题目内容
14.某家公司每月生产两种布料A和B,所有原料是三种不同颜色的羊毛.下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量.| 羊毛颜色 | 每匹需要/kg | 供应量/kg | |
| 布料A | 布料B | ||
| 红 | 3 | 3 | 1050 |
| 绿 | 4 | 2 | 1200 |
| 黄 | 2 | 6 | 1800 |
(Ⅰ)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)如何安排生产才能使得利润最大?并求出最大的利润.
分析 (Ⅰ)根据条件建立不等式关系,利用二元一次不等式组表示平面区域进行作图即可.
(Ⅱ)求出目标函数,利用线性规划的知识进行求解.
解答 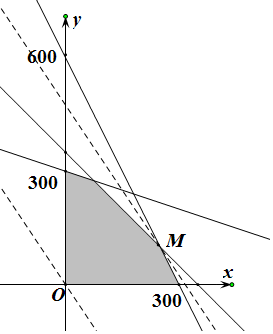 解:(Ⅰ)设每月生产布料A、B分别为x匹、y匹,利润为Z元,
解:(Ⅰ)设每月生产布料A、B分别为x匹、y匹,利润为Z元,
则$\left\{\begin{array}{l}{3x+3y≤1050}\\{4x+2y≤1200}\\{2x+6y≤1800}\\{x≥0,y≥0}\end{array}\right.$,对应的可行域如图:
(Ⅱ)设最大利润为z,则目标函数为 z=60x+40y,
则y=-$\frac{3}{2}$x+$\frac{z}{40}$,平移直线y=-$\frac{3}{2}$x+$\frac{z}{40}$,当直线y=-$\frac{3}{2}$x+$\frac{z}{40}$经过可行域上M时,截距最大,即z最大.
解方程组$\left\{\begin{array}{l}{3x+3y=1050}\\{4x+2y=1200}\end{array}\right.$,
得M的坐标为x=250,y=100
所以zmax=60x+40y=19000.
答:该公司每月生产布料A、B分别为250、100匹时,能够产生最大的利润,最大的利润是19000 元.
点评 本题主要考查线性规划的应用,建立约束条件,利用线性规划的知识进行求解是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.$\int_2^3{(2x+1)dx=}$( )
| A. | 2 | B. | 6 | C. | 10 | D. | 8 |
2.曲线$y={x^2}+x+\frac{1}{2}$在$({0,\frac{1}{2}})$处的切线方程为( )
| A. | $y=-x+\frac{1}{2}$ | B. | $y=x+\frac{1}{2}$ | C. | $y=-2x+\frac{1}{2}$ | D. | $y=2x+\frac{1}{2}$ |
3.在等差数列{an}中,S10=120,那么a1+a10的值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |