函数f的图象如图所示.则( )A．$\frac{1}{2}$为f(x)的极大值点B．-2为f(x)的极大值点C．2为f(x)的极大值D．$\frac{4}{5}$为f(x)的极小值点题目和参考答案——青夏教育精英家教网—

题目内容

7．函数f（x）的导函数f′（x）的图象如图所示，则（　　）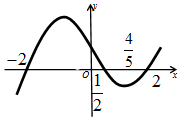

	A．	$\frac{1}{2}$为f（x）的极大值点		B．	-2为f（x）的极大值点
	C．	2为f（x）的极大值		D．	$\frac{4}{5}$为f（x）的极小值点

分析利用导函数的图象，判断导函数的极值点，推出结果即可．

解答解：由导函数的图象可知：x＜-2时，函数是减函数，x∈（-2，$\frac{1}{2}$），函数是增函数；x∈（$\frac{1}{2}，2$）时，函数是减函数，x＞2时函数是增函数，
所以，$\frac{1}{2}$为f（x）的极大值点．
故选：A．

点评本题考查电话上的图象的应用，函数的单调性以及函数的极值的判断，基本知识的考查．

练习册系列答案

18．要得到$y=cos（4x-\frac{π}{3}）$的图象，只需将函数y=cos4x图象（　　）

	A．	向左平移$\frac{π}{12}$个单位		B．	向右平移$\frac{π}{12}$个单位
	C．	向左平移$\frac{π}{3}$个单位		D．	向右平移$\frac{π}{3}$个单位

15．用适当的方法证明下列命题：
（1）$\sqrt{b+1}-\sqrt{b}＜\sqrt{b-1}-\sqrt{b-2}（b≥2）$
（2）设a，b，c∈（0，+∞），求证：三个数中$a+\frac{1}{b}，c+\frac{1}{a}，b+\frac{1}{c}$至少有一个不小于2．

2．曲线$y={x^2}+x+\frac{1}{2}$在$（{0，\frac{1}{2}}）$处的切线方程为（　　）

12．复数i（1+i）（i为虚数单位）的实部为-1．

3．在等差数列{a_n}中，S₁₀=120，那么a₁+a₁₀的值是（　　）

20．下列命题中真命题的个数为（　　）
①用数学归纳法证明1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n-1}$＜n（n∈N^*，且n＞1）时，第一步即证不等式1+$\frac{1}{3}$＜2成立；
②若关于x的不等式ax²-|x|+a＜0的解集为空集，则a的取值范围为[$\frac{1}{2}$，+∞）
③若命题p：?n∈N，2ⁿ＞1000，则￢p：?n∈N，2ⁿ＜1000
④命题若“x（y-1）=0，则x=0或y=1”的逆否命题是“若x≠0且y≠1，则x（y-1）≠0”

1．椭圆$\frac{x^2}{5}+\frac{y^2}{4}=1$的焦距是（　　）

试题分类