题目内容
已知圆C和直线3x-4y-11=0以及x轴都相切,且过点(6,2),求圆C的方程.
考点:直线与圆的位置关系
专题:直线与圆
分析:设出圆的标准方程,利用待定系数法求出圆心和半径即可.
解答:
解:设圆心坐标为(a,b),半径R,
∵圆C和x轴相切,∴R=|b|,
则圆C的方程为(x-a)2+(y-b)2=b2 (b>0)
∵过点(6,2),
∴(6-a)2+(2-b)2=b2 (b>0)
即(6-a)2+4-4b=0,①
∵圆与直线3x-4y-11=0相切,
∴圆心到直线的距离d=
=|b|,②
联立方程组解得
或
,
故圆C的方程为(x-2)2+(y-5)2=25 或(x+2)2+(y-17)2=289.
∵圆C和x轴相切,∴R=|b|,
则圆C的方程为(x-a)2+(y-b)2=b2 (b>0)
∵过点(6,2),
∴(6-a)2+(2-b)2=b2 (b>0)
即(6-a)2+4-4b=0,①
∵圆与直线3x-4y-11=0相切,
∴圆心到直线的距离d=
| |3a-4b-11| |
| 5 |
联立方程组解得
|
|
故圆C的方程为(x-2)2+(y-5)2=25 或(x+2)2+(y-17)2=289.
点评:本题主要考查圆的方程的求解,根据直线和圆的位置关系求出圆心和半径是解决本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知圆O:x2+y2=1,直线l:3x+4y-3=0,则直线l被圆O所截的弦长为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
一个箱子中装有9张卡片,分别标有数字1,2,3,…,9,现在有放回地依次抽取3张,然后按抽取的先后顺序依次构成一个三位数,则这三位数中恰有两个数字重复的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
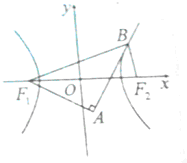 如图,F1,F2分别是双曲线
如图,F1,F2分别是双曲线