题目内容
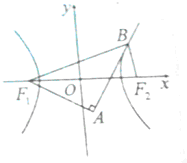 如图,F1,F2分别是双曲线
如图,F1,F2分别是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求该双曲线的离心率;
(2)若a=1,双曲线上的一点B满足以F1B为直径的圆过点A(
| ||
| 2 |
| ||
| 2 |
考点:双曲线的简单性质
专题:计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出双曲线的渐近线方程,由条件可得c2=2b2,再由A,B,C的关系和离心率公式,即可计算得到;
(2)求出双曲线方程,运用直线垂直的条件,解方程求得B的坐标,求出直线AB,F1B,F2B的斜率,运用到角公式计算即可得证.
(2)求出双曲线方程,运用直线垂直的条件,解方程求得B的坐标,求出直线AB,F1B,F2B的斜率,运用到角公式计算即可得证.
解答:
(1)解:双曲线
-
=1的渐近线方程为y=±
x,
由渐近线方程为y=±kx(k>0),且该双曲线的离心率e=
k,
则有k=
,e=
=
•
,即有c2=2b2=2(c2-a2),即有c2=2a2,
则有离心率e=
;
(2)证明:由a=1,e=
,可得,c=
,b=1.
则双曲线方程为x2-y2=1,F1(-
,0),F2(
,0),
设B(m,n),则由以F1B为直径的圆过点A,
即有AB⊥F1A,则
•
=-1,
即有3m-n=2
,又m2-n2=1.
解得,m=
,n=
.
则B(
,
),
则有kAB=
=3,kF1B=
=
,kF2B=
=-1.
则F1B到AB的角的正切为
=2,AB到F2B的角的正切为
=2,
则有∠ABF1=∠ABF2,即有AB平分∠F1BF2.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
由渐近线方程为y=±kx(k>0),且该双曲线的离心率e=
| 2 |
则有k=
| b |
| a |
| c |
| a |
| 2 |
| b |
| a |
则有离心率e=
| 2 |
(2)证明:由a=1,e=
| 2 |
| 2 |
则双曲线方程为x2-y2=1,F1(-
| 2 |
| 2 |
设B(m,n),则由以F1B为直径的圆过点A,
即有AB⊥F1A,则
n+
| ||||
m-
|
| ||||
-
|
即有3m-n=2
| 2 |
解得,m=
3
| ||
| 4 |
| ||
| 4 |
则B(
3
| ||
| 4 |
| ||
| 4 |
则有kAB=
| ||||||||
|
| ||||||
|
| 1 |
| 7 |
| ||||||
|
则F1B到AB的角的正切为
3-
| ||
1+
|
| -1-3 |
| 1+(-3) |
则有∠ABF1=∠ABF2,即有AB平分∠F1BF2.
点评:本题考查双曲线的方程和性质,考查渐近线方程和离心率的求法,考查直线到直线的角的公式,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知圆C:x2+y2=10,过点P(1,3)作圆C的切线,则切线方程为( )
| A、x+3y-10=0 |
| B、x-3y+8=0 |
| C、3x+y-6=0 |
| D、3x-y+10=0 |
 从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩,得到如下茎叶图.已知甲班样本成绩的中位数为13,乙班样本成绩的平均数为16.
从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩,得到如下茎叶图.已知甲班样本成绩的中位数为13,乙班样本成绩的平均数为16.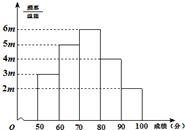 有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示: