题目内容
一个箱子中装有9张卡片,分别标有数字1,2,3,…,9,现在有放回地依次抽取3张,然后按抽取的先后顺序依次构成一个三位数,则这三位数中恰有两个数字重复的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:先求出总得事件数共有729种,三位数中恰有两个数字重复,每种数字都有重复的可能,从9个数字中任1个,再从剩下的8个中再选一个,每一种选法有3种排列,继而求出三位数中恰有两个数字重复,根据概率公式计算即可
解答:
解:有放回地依次抽取3张,共有9×9×9=729种,
三位数中恰有两个数字重复,每种数字都有重复的可能,从9个数字中任1个,再从剩下的8个中再选一个,每一种选法有3种排列,
故这三位数中恰有两个数字重复共有9×8×3=216,
故这三位数中恰有两个数字重复的概率P=
=
,
故选:C
三位数中恰有两个数字重复,每种数字都有重复的可能,从9个数字中任1个,再从剩下的8个中再选一个,每一种选法有3种排列,
故这三位数中恰有两个数字重复共有9×8×3=216,
故这三位数中恰有两个数字重复的概率P=
| 216 |
| 729 |
| 8 |
| 27 |
故选:C
点评:本题考查了古典概型概率的求法,关键是找到,三位数中恰有两个数字重复的种数,属于基础题

练习册系列答案
相关题目
椭圆
+
=1上的一点P到椭圆一个焦点的距离为5,则点P到另一个焦点的距离为( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、7 | B、5 | C、4 | D、1 |
已知等差数列{an},则“a2>a1”是“数列{an}为单调递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
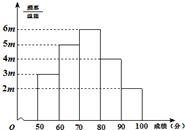 有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示: