题目内容
若一个圆锥的底面半径为1，侧面积是底面积的2倍，则该圆锥的体积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由已知中，圆锥的底面半径为1，侧面积是底面积的2倍，分析圆锥的母线长，进而求出圆锥的高，结合圆锥的体积公式即可获得问题的解答．
解答：
解：∵圆锥的底面半径r=1，侧面积是底面积的2倍，
∴圆锥的母线长l=2，
故圆锥的高h=
=
，
故圆锥的体积V=
Sh=
πr2•h=
，
故答案为：
．
∴圆锥的母线长l=2，
故圆锥的高h=
| l2-r2 |
| 3 |
故圆锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查的是圆锥的体积求解问题．在解答的过程当中充分体现了圆锥体积公式的应用以及转化思想的应用．值得同学们体会反思．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
如图，若在矩形OABC中随机一粒豆子，则豆子落在图中阴影部分的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
从甲、乙两班某项测试成绩中各随机抽取5名同学的成绩，得到如下茎叶图．已知甲班样本成绩的中位数为13，乙班样本成绩的平均数为16．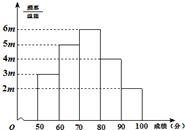
有20名学生参加某次考试，成绩（单位：分）的频率分布直方图如图所示：