题目内容
已知抛物线y2=4x的焦点为F,直线x=t(t>0,且t≠1)与抛物线交于A,B两点(点A在第一象限),定点Q的坐标为(-1,0),直线QA与抛物线的另一个交点为点M.
(1)求证:点M,F,B三点共线;
(2)当2≤t≤3时,求
的取值范围.
(1)求证:点M,F,B三点共线;
(2)当2≤t≤3时,求
| |MA| |
| |MB| |
考点:抛物线的简单性质
专题:向量与圆锥曲线,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)首先设出直线QA的方程为:x=my-1联立抛物线得:
得到直线BM的方程y-y2=
(x-x2)进一步求得F在直线上,以此三点共线.
(2)由(1)的结论分别求得
|和|
|,进一步利用导数求得2≤t≤3时函数为单调递增函数,最后确定
的取值范围.
|
| y2+y1 |
| x2-x1 |
(2)由(1)的结论分别求得
| |MA |
| MB |
|
| ||
|
|
解答:
(1)证明:已知抛物线y2=4x的焦点为F,直线x=t(t>0,且t≠1)与抛物线交于A,B两点(点A在第一象限),定点Q的坐标为(-1,0),直线QA与抛物线的另一个交点为点M.
设:A(x1,y1) M(x2,y2) B(x1,-y1),则直线QA的方程为:x=my-1
与抛物线y2=4x联立得到:
所以:y2-4my+4=0
y1+y2=4m y1•y2=4
则直线BM的方程为:
y-y2=
(x-x2)
即:y-y2=
(x-x2)
令y=0解得:x=
=1
即:焦点F(1,0)
所以:点M,F,B三点共线
(2)解:由(1)得:A(t,2
)B(t,-2
)Q(-1,0)
则利用A、M、Q三点共线求得:M(
,
)
|
|=
|
|=
=
设(t+
)2+4(t+
)=x则:
=
=
利用导数得:2≤t≤3函数为增函数,
≤x≤
进一步求得:
∈[
,
]
故答案为:(1)略
(2)
∈[
,
]
设:A(x1,y1) M(x2,y2) B(x1,-y1),则直线QA的方程为:x=my-1
与抛物线y2=4x联立得到:
|
所以:y2-4my+4=0
y1+y2=4m y1•y2=4
则直线BM的方程为:
y-y2=
| y2+y1 |
| x2-x1 |
即:y-y2=
| 4 |
| y2-y1 |
令y=0解得:x=
| y1y2 |
| 4 |
即:焦点F(1,0)
所以:点M,F,B三点共线
(2)解:由(1)得:A(t,2
| t |
| t |
则利用A、M、Q三点共线求得:M(
| 1 |
| t |
| 2 | ||
|
|
| MA |
(t-
|
|
| MB |
(t-
|
|
| ||
|
|
|
| 1 |
| t |
| 1 |
| t |
|
| ||
|
|
|
1-
|
利用导数得:2≤t≤3函数为增函数,
| 65 |
| 4 |
| 220 |
| 9 |
进一步求得:
|
| ||
|
|
| ||
| 9 |
| ||
| 16 |
故答案为:(1)略
(2)
|
| ||
|
|
| ||
| 9 |
| ||
| 16 |
点评:本题考查的知识要点:直线与圆锥曲线的关系,三点共线的充要条件,向量的坐标运算,及向量的模,导数在函数单调性中的应用,利用单调性求
的值域
|
| ||
|
|

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
已知集合A={y|y=log2x,x>1},B={y|y=(
)x,x>1},则(∁RA)∪B=( )
| 1 |
| 2 |
A、{y|y<
| ||
| B、{y|y≤0或y>1} | ||
C、{y|
| ||
| D、R |
 如图,在?ABCD中,已知AB=2,AD=1,∠DAB=60°,M为DC的中点.
如图,在?ABCD中,已知AB=2,AD=1,∠DAB=60°,M为DC的中点.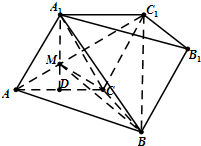 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.