题目内容
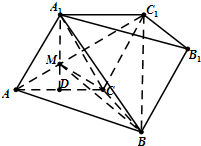 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.(Ⅰ)求证:A1B⊥AC1;
(Ⅱ)设直线AC1与A1D分别交于点M,求三棱锥C1-MBC的体积.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)通过证明BC⊥AC1,A1C⊥AC1,证出AC1⊥平面A1BC,即证AC1⊥A1B;
(Ⅱ)利用V三棱锥C1-ABC与V三棱锥M-ABC的关系,求出V三棱锥C1-MBC的大小.
(Ⅱ)利用V三棱锥C1-ABC与V三棱锥M-ABC的关系,求出V三棱锥C1-MBC的大小.
解答:
解:(Ⅰ)∵A1D⊥平面ABC,BC?平面ABC,
∴A1D⊥BC;
又∵BC⊥AC,且A1D∩AC=D,
∴BC⊥平面A1ACC1,
∴BC⊥AC1;①
又∵四边形A1ACC1为菱形,
∴A1C⊥AC1;②
由①②得,AC1⊥平面A1BC,
且A1B?平面A1BC,
∴AC1⊥A1B;
(Ⅱ)∵D是线段AC的中点,∴
=
,
∴
=
,即
=
;
∴V三棱锥C1-MBC=V三棱锥C1-ABC-V三棱锥M-ABC
=3V三棱锥M-ABC-V三棱锥M-ABC=2V三棱锥M-ABC
=2×
×S△ABC•MD
又S△ABC=
×2×2=2,
MD=
×A1D=
×
=
;
∴V三棱锥C1-MBC=2×
×2×
=
.
∴A1D⊥BC;
又∵BC⊥AC,且A1D∩AC=D,
∴BC⊥平面A1ACC1,
∴BC⊥AC1;①
又∵四边形A1ACC1为菱形,
∴A1C⊥AC1;②
由①②得,AC1⊥平面A1BC,
且A1B?平面A1BC,
∴AC1⊥A1B;
(Ⅱ)∵D是线段AC的中点,∴
| AD |
| A1C1 |
| 1 |
| 2 |
∴
| AM |
| MC1 |
| 1 |
| 2 |
| C1M |
| C1A |
| 2 |
| 3 |
∴V三棱锥C1-MBC=V三棱锥C1-ABC-V三棱锥M-ABC
=3V三棱锥M-ABC-V三棱锥M-ABC=2V三棱锥M-ABC
=2×
| 1 |
| 3 |
又S△ABC=
| 1 |
| 2 |
MD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
∴V三棱锥C1-MBC=2×
| 1 |
| 3 |
| ||
| 3 |
| 4 |
| 9 |
| 3 |
点评:本题考查了空间中的垂直关系的应用问题,也考查了计算空间几何体的体积的问题,是中档题.

练习册系列答案
相关题目
若一直线上有一点在已知平面外,则下列结论中正确的是( )
| A、直线与平面平行 |
| B、直线与平面相交 |
| C、直线上至少有一个点在平面内 |
| D、直线上有无数多个点都在平面外 |
已知函数f(x)=
,若|f(x)|≥ax,则a的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,1] |
| C、[-2,1] |
| D、[-2,0] |