题目内容
如图，在?ABCD中，已知AB=2，AD=1，∠DAB=60°，M为DC的中点．（1）求
| AM |
| BD |
（2）设
| AP |
| AB |
考点：平面向量数量积的运算,向量加减混合运算及其几何意义
专题：平面向量及应用
分析：（1）设
=
，
=
，可得
•
=|
||
|•cos60°．再利用向量的三角形法则、数量积运算即可得出；
（2）利用向量的三角形法则、向量垂直与数量积的关系即可得出．
| AD |
| a |
| AB |
| b |
| a |
| b |
| a |
| b |
（2）利用向量的三角形法则、向量垂直与数量积的关系即可得出．
解答：
解：（1）设
=
，
=
，∴
•
=|
||
|•cos60°=1×2×
=1．
=
+
=
+
，
=
-
=
-
．
∴
•
=(
+
)•(
-
)=
2-
•
-
2=1-
×1-
×22=-
．
（2）
=
+
，
=
+
=-
+λ
．
∵
⊥
，
∴
•
=(
+
)•(-
+λ
)=0，
化为-
2+(λ-1)
•
+λ
2=0，
∴-1+（λ-1）×1+4λ=0，
解得λ=
．
| AD |
| a |
| AB |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| AM |
| AD |
| DM |
| a |
| 1 |
| 2 |
| b |
| BD |
| AD |
| AB |
| a |
| b |
∴
| AM |
| BD |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| a |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
（2）
| AC |
| a |
| b |
| DP |
| DA |
| AP |
| a |
| b |
∵
| AC |
| DP |
∴
| AC |
| DP |
| a |
| b |
| a |
| b |
化为-
| a |
| a |
| b |
| b |
∴-1+（λ-1）×1+4λ=0，
解得λ=
| 2 |
| 5 |
点评：本题考查了向量的三角形法则、向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
小明早晨去上学，由于担心迟到被老师批评，所以一开始就跑步，等跑累了再走完余下的路程．如果用纵轴表示小明离学校的距离，横轴表示出发后的时间，则下列四个图形中比较符合小明走法的是哪一个呢？（ ）
A、 |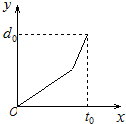
B、 |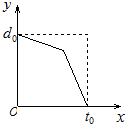
C、 |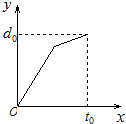
D、 |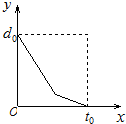
将甲、乙、丙、丁、戊5名大学生分配到3个乡镇去当村官，设事件A为“每个乡镇至少有一名大学生村官”，事件B为“甲、乙、丙三人在同一个乡镇当村官”，则概率P（B|A）等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设随机变量X～N（1，4），且P（X≤a）=P（X＞2），则实数a的值为（ ）
| A、3 | B、2 | C、1 | D、0 |