题目内容
12.一袋中装有5个白球,3个红球,现从袋中往外取球,每次任取一个,取出后记下颜色,若为红色则停止,若为白色则继续抽取,设停止时从袋中抽取的白球的个数为随机变量X,则P(x≤$\sqrt{6}$)=$\frac{23}{28}$,E(x)=$\frac{5}{4}$,V(x)=$\frac{27}{16}$.分析 X=k表示前k个球为白球,第k+1个恰为红球,由题意X的可能取值为0,1,2,3,4,5,分别求出相应的概率,由此能求出ξ的分布列,从而能求出结果.
解答 解:X=k表示前k个球为白球,第k+1个恰为红球,
P(X=0)=$\frac{{A}_{3}^{1}}{{A}_{8}^{1}}$=$\frac{3}{8}$,
P(X=1)=$\frac{{A}_{5}^{1}{A}_{3}^{1}}{{A}_{8}^{2}}$=$\frac{15}{56}$,
P(X=2)=$\frac{{A}_{5}^{2}{A}_{3}^{1}}{{A}_{8}^{3}}$=$\frac{10}{56}$,
P(X=3)=$\frac{{A}_{5}^{3}{A}_{3}^{1}}{{A}_{8}^{4}}$=$\frac{6}{56}$,
P(X=4)=$\frac{{A}_{5}^{4}{A}_{3}^{1}}{{A}_{8}^{5}}$=$\frac{3}{56}$,
P(X=5)=$\frac{{A}_{5}^{5}{A}_{3}^{1}}{{A}_{8}^{6}}$=$\frac{1}{56}$,
∴ξ的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{8}$ | $\frac{15}{56}$ | $\frac{10}{56}$ | $\frac{6}{56}$ | $\frac{3}{56}$ | $\frac{1}{56}$ |
=$\frac{3}{8}$+$\frac{15}{56}$+$\frac{10}{56}$=$\frac{23}{28}$.
E(X)=$0×\frac{3}{8}+1×\frac{15}{56}+2×\frac{10}{56}+3×\frac{6}{56}+4×\frac{3}{56}$+5×$\frac{1}{56}$=$\frac{5}{4}$.
V(X)=(0-$\frac{5}{4}$)2×$\frac{3}{8}$+(1-$\frac{5}{4}$)2×$\frac{15}{56}$+(2-$\frac{5}{4}$)2×$\frac{10}{56}$+$(3-\frac{5}{4})^{2}×\frac{6}{56}$+(4-$\frac{5}{4}$)2×$\frac{3}{56}$+(5-$\frac{5}{4}$)2×$\frac{1}{56}$=$\frac{27}{16}$.
故答案为:$\frac{23}{28}$,$\frac{5}{4}$,$\frac{27}{16}$.
点评 本题考查概率的求法,考查离散型随机变量的数学期望、方差的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
2.已知集合M={x|x>0},N={x|x2≤4},则集合M∩N=( )
| A. | {x|-2<x<0} | B. | {x|0<x≤2} | C. | {x|-2<x<2} | D. | {x|x>-2} |
1.如图是某算法的程序框图,若输出y值为4,则输入的x最大负整数是( )


| A. | -3 | B. | -2 | C. | -1 | D. | -4 |
2.已知复数z1,z2,则下列说法中正确的是( )
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
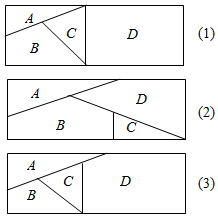 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色. 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.