题目内容
7.求经过点A(5,2),B(3,2),圆心在直线2x-y-3=0上的圆的方程.分析 由A和B的坐标求出直线AB的斜率,根据两直线垂直斜率的乘积为-1求出直线AB垂直平分线的斜率,根据垂径定理得到圆心在弦AB的垂直平分线上,又圆心在已知直线上,联立两直线方程组成方程组,求出方程组的解集,得到圆心M的坐标,再利用两点间的距离公式求出|AM|的长,即为圆的半径,由圆心坐标和半径写出圆的标准方程即可.
解答 解:∵A(5,2),B(3,2),
∴直线AB的斜率为$\frac{2-2}{5-3}$=0,
∴直线AB垂直平分线与x轴垂直,其方程为:x=$\frac{5+3}{2}$=4,
与直线2x-y-3=0联立解得:x=4,y=5,即所求圆的圆心M坐标为(4,5),
又所求圆的半径r=|AM|=$\sqrt{(5-4)^{2}+(2-5)^{2}}$=$\sqrt{10}$,
则所求圆的方程为(x-4)2+(y-5)2=10.
点评 本题考查了圆的标准方程,涉及的知识有:直线斜率的求法,两直线垂直时斜率满足的关系,两点间的距离公式,以及两直线的交点坐标求法,其中根据垂径定理得出弦AB的垂直平分线过圆心是解本题的关键,是基础题.

练习册系列答案
相关题目
17.集合M={x|0≤x<2},集合N={x|x2+2x-3<0},则集合M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
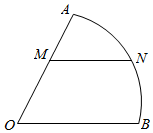 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.