题目内容
17. 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.(1)求证:AN∥平面MEC;
(2)求三棱锥E-CMN的体积.
分析 (1)设MC,BN交于F,连结EF,由四边形BCNM是平行四边形可得F是BN的中点,由中位线定理得EF∥AN,故AN∥平面MEC;
(2)VE-CMN=$\frac{1}{2}$VA-CMN=$\frac{1}{2}$VC-ANM=$\frac{1}{2}$VB-ANM=$\frac{1}{2}$VN-MAB=$\frac{1}{2}$VD-MAB=$\frac{1}{2}$VM-ABD.
解答 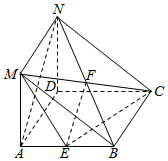 证明:(1)设MC,BN交于F,连结EF,
证明:(1)设MC,BN交于F,连结EF,
∵四边形BCNM是平行四边形,
∴F是BN的中点,∵E是AB的中点,
∴EF∥AN,
又AN?平面MEC,EF?平面MEC,
∴AN∥平面MEC.
(2)∵E是AB的中点,∴VE-CMN=$\frac{1}{2}$VA-CMN=$\frac{1}{2}$VC-ANM.
∵BC∥平面ADNM,∴VC-ANM=VB-ANM=VN-MAB,
∵ND∥平面ABM,∴VN-MAB=VD-MAB=VM-ABD.
∵平面ADNM⊥平面ABCD,平面ADNM∩平面ABCD=AD,MA⊥AD,
∴MA⊥平面ABCD,
∵S△ABD=$\frac{1}{2}AB•AD•sin∠BAD$=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴VM-ABD=$\frac{1}{3}{S}_{△ABD}•AM$=$\frac{1}{3}×\sqrt{3}×1=\frac{\sqrt{3}}{3}$.
∴VE-CMN=$\frac{1}{2}$VM-ABD=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
7.在下面给出的四个函数中,既是区间(0,$\frac{π}{2}$)上的增函数,又是以π为周期的偶函数的是( )
| A. | y=|sinx| | B. | y=|cosx| | C. | y=sin2x | D. | y=cos2x |
5.已知直线l过点(0,-4),P是l上的一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,A,B是切点,若四边形PACB的最小面积是2,则直线的斜率为( )
| A. | $±\sqrt{2}$ | B. | ±$\frac{\sqrt{21}}{2}$ | C. | ±2$\sqrt{2}$ | D. | ±2 |
9.已知数列{an}的通项公式为an=$\frac{n-\sqrt{51}}{n-\sqrt{52}}$,则在数列{an}的前30项中,最大项和最小项分别是( )
| A. | a30,a1 | B. | a1,a30 | C. | a8,a30 | D. | a8,a7 |
6.随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对公务员和教师各抽取了50人进行调查,将调查情况进行整理后制成下表:
附:
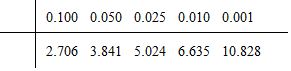
(Ⅰ)求上表中m,n,p的值,并问是否有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为x,求x的分布列和期望.
| 公务员 | 教师 | 合计 | |
| 同意延迟退休 | 40 | n | 70 |
| 不同意延迟退休 | m | 20 | p |
| 合计 | 50 | 50 | 100 |
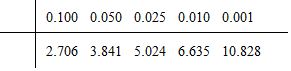
(Ⅰ)求上表中m,n,p的值,并问是否有95%的把握认为“是否同意延迟退休与不同的职业有关”.
(Ⅱ)现用分层抽样方法(按同意和不同意分二层)从调查的两个职业人群中各抽取五人,然后从每个职业的五人中各抽取两人,将这四人中的同意延迟退休的人数记为x,求x的分布列和期望.