题目内容
3. 用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.
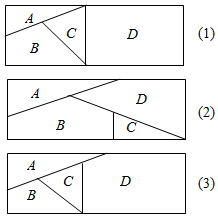
用n(n∈N*)种不同颜色给如图的4个区域涂色,要求相邻区域不能用同一种颜色.(1)当n=6时,图(1)、图(2)各有多少种涂色方案?(要求:列式或简述理由,结果用数字作答);
(2)若图(3)有180种涂色法,求n的值.
分析 (1)如图(1)据题意,分四个步骤来完成,由乘法原理计算可得答案.
图(2)分两类,若A,C相同,若A,C不同,根据分类计数原理可得.
(2)A有n种方法,B有n-1种方法,C有n-2种方法,D有n-2种方法,共有涂色方法n(n-1)(n-2)(n-2)=180,计算可得答案.
解答 解:(1)当n=6时,图(1)A有6种方法,B有5种方法,C有4种方法,D有5种方法,共有涂色方法6×5×4×5=600种
图(2)若A,C相同,则A有6种方法,B有5种方法,D有4种方法,共有6×5×4=120种
若A,C不同,则A有6种方法,B有5种方法,C有4种方法,D有3种方法,共有6×5×4×3=360种
∴共有涂色方法120+360=480种.
(2)A有n种方法,B有n-1种方法,C有n-2种方法,D有n-2种方法,共有涂色方法n(n-1)(n-2)(n-2)种
由n(n-1)(n-2)(n-2)=180
解得n=5
点评 本题考查涂色问题,是排列、组合的典型题目,一般涉及分类加法原理与分步乘法原理,注意认真分析题意,把握好限制条件.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
11.某人射击1次,命中8~10环的概率如表所示:
则他射击1次,至少命中9环的概率为0.3.
| 命中环数 | 10环 | 9环 | 8环 |
| 概 率 | 0.12 | 0.18 | 0.28 |
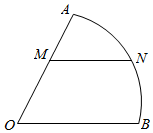 如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.
如图,扇形AOB是某个旅游景点的平面示意图,圆心角AOB的大小等于$\frac{π}{3}$,半径OA=200m,点M在半径OA上,点N在$\widehat{AB}$上,且MN∥OB,求观光道路OM与MN长度之和的最大值.