题目内容
 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若PA=1,AD=2,求二面角B-PC-A的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由BD⊥AC,PA⊥BD,利用线面垂直的判定即可证明;(Ⅱ)作BE⊥PC,连接OE,证明∠BE0即二面角B-PC-A的平面角,后在相应的直角三角形中计算.
解答:
 (Ⅰ)证明:∵底面ABCD为正方形,∴BD⊥AC,PA⊥平面ABCD,PA⊥BD,AC∩PA=A,∴BD⊥平面PAC;
(Ⅰ)证明:∵底面ABCD为正方形,∴BD⊥AC,PA⊥平面ABCD,PA⊥BD,AC∩PA=A,∴BD⊥平面PAC;
(Ⅱ)解:AC⊥BD=O,作BE⊥PC,连接OE,由(Ⅰ)知BD⊥平面PAC,PC?平面PAC,∴BD⊥PC,BE∩BD=B,∴PC⊥面BDE,∴OE⊥PC,∴∠BE0即二面角B-PC-A的平面角.∵底面ABCD为正方形,AD=2,∴AC=2
,在Rt△PAC中,PA=1,AC=2
,PC=3,sin∠PCA=
,在Rt△OEC中,OC=
,sin∠PCA=
,∴OE=
,在Rt△BOE中,OE=
,BO=
,BE=
∴cos∠BE0=
=
,∴二面角B-PC-A的余弦值为
.
 (Ⅰ)证明:∵底面ABCD为正方形,∴BD⊥AC,PA⊥平面ABCD,PA⊥BD,AC∩PA=A,∴BD⊥平面PAC;
(Ⅰ)证明:∵底面ABCD为正方形,∴BD⊥AC,PA⊥平面ABCD,PA⊥BD,AC∩PA=A,∴BD⊥平面PAC;(Ⅱ)解:AC⊥BD=O,作BE⊥PC,连接OE,由(Ⅰ)知BD⊥平面PAC,PC?平面PAC,∴BD⊥PC,BE∩BD=B,∴PC⊥面BDE,∴OE⊥PC,∴∠BE0即二面角B-PC-A的平面角.∵底面ABCD为正方形,AD=2,∴AC=2
| 2 |
| 2 |
| 1 |
| 3 |
| 2 |
| OE |
| OC |
| ||
| 3 |
| ||
| 3 |
| 2 |
| ||
| 3 |
| OE |
| BE |
| ||
| 10 |
| ||
| 10 |
点评:本题考查线面垂直,面面角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
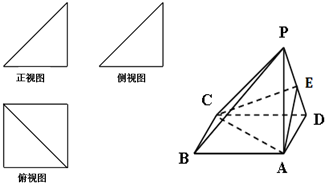 一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.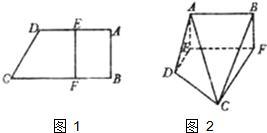 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.