题目内容
二元一次方程组
=λ
有非零解，则λ= ．
|
|
|
考点：矩阵与向量乘法的意义
专题：矩阵和变换
分析：方程组有非零解，那么λ是矩阵
的特征值，由此能求出结果．
|
解答：
解：方程组有非零解，那么λ是矩阵
的特征值，
由|A-λE|=
-λE=（2-λ）（3-λ）-2=（λ-1）（λ-4）=0，
解得λ=1或λ=4，
所以，当 λ=1或λ=4 时，方程组有非零解．
故答案为：1或4．
|
由|A-λE|=
|
解得λ=1或λ=4，
所以，当 λ=1或λ=4 时，方程组有非零解．
故答案为：1或4．
点评：本题考查实数值的求法，是基础题，解题时要注意矩阵的特征值的合理运用．
练习册系列答案
相关题目
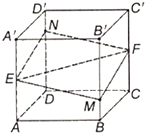如图所示，正方体ABCD-A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线E，F的平面分别与棱BB′、DD′交于M，N，设BM=x，x∈[0，1]，给出以下五个命题：