题目内容
已知f（k）=k+（k+1）+（k+2）+…+2k（k∈N*），则f（k+1）-f（k）= ．
考点：函数的值
专题：函数的性质及应用
分析：写出f（k+1）-f（k）的表达式求解即可．
解答：
解：f（k）=k+（k+1）+（k+2）+…+2k（k∈N*），
则f（k+1）-f（k）=（k+1）+（k+2）+（k+3）+…+（2k-1）+（2k）+（2k+1）+2（k+1）-[k+（k+1）+（k+2）+…+2k]
=3（k+1）
故答案为：3（k+1）
则f（k+1）-f（k）=（k+1）+（k+2）+（k+3）+…+（2k-1）+（2k）+（2k+1）+2（k+1）-[k+（k+1）+（k+2）+…+2k]
=3（k+1）
故答案为：3（k+1）
点评：正确弄清由k到k+1时增加和减少的项是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
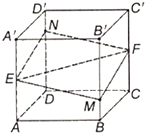如图所示，正方体ABCD-A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线E，F的平面分别与棱BB′、DD′交于M，N，设BM=x，x∈[0，1]，给出以下五个命题：
向量