题目内容
已知数列{an}中，a9=
，an+1=
．
（1）求证：数列{
}为等差数列；
（2）求an．
| 1 |
| 7 |
| an |
| 3an+1 |
（1）求证：数列{
| 1 |
| an |
（2）求an．
考点：数列递推式,等差关系的确定
专题：计算题,等差数列与等比数列
分析：（1）取倒数，即可证明数列{
}为等差数列；
（2）先求数列{
}的通项，再求an．
| 1 |
| an |
（2）先求数列{
| 1 |
| an |
解答：
（1）证明：∵an+1=
，
∴
=
，
∴
=3+
，
∴
-
=3
故数列{
}为等差数列；
（2）解：∵
=
+(n-9)d=7+(n-9)×3=3n-20，
∴an=
．
| an |
| 3an+1 |
∴
| 1 |
| an+1 |
| 3an+1 |
| an |
∴
| 1 |
| an+1 |
| 1 |
| an |
∴
| 1 |
| an+1 |
| 1 |
| an |
故数列{
| 1 |
| an |
（2）解：∵
| 1 |
| an |
| 1 |
| a9 |
∴an=
| 1 |
| 3n-20 |
点评：本题考查等差数列的证明，考查数列的通项，确定数列{
}为等差数列是关键．
| 1 |
| an |
练习册系列答案
相关题目
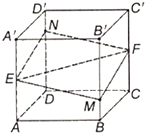如图所示，正方体ABCD-A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线E，F的平面分别与棱BB′、DD′交于M，N，设BM=x，x∈[0，1]，给出以下五个命题：