题目内容

7．．函数y=2sinxcosx的导数为（　　）
A．y′=cosxB．y′=2cos2xC．y′=2（sin2x-cos2x）D．y′=-sin2x

分析 根据导数的运算法则求导即可．

解答 解：y′=2（cos2x-sin2x）=2cos2x，
故选：B

点评 本题考查导数的运算法则，属于基础题．

练习册系列答案
相关题目
17．函数$f（x）=\frac{1}{2}{x^2}-lnx$的单调减区间（　　）
A．（-1，1]B．（0，1]C．（1，+∞）D．（0，+∞）
18．已知向量$\overrightarrow a=（1，-2）$，向量$\overrightarrow b$满足$|{\overrightarrow b}|=2$，$\overrightarrow a•\overrightarrow b$夹角为$\frac{π}{3}$，则$\overrightarrow a•\overrightarrow b$=（　　）
A．$\sqrt{5}$B．2C．$\sqrt{3}$D．$\sqrt{2}$
15．已知椭圆C的中心为原点O，焦点在x轴上，且经过点${A_1}（-2，0），{A_2}（\sqrt{2}，\frac{{\sqrt{2}}}{2}）$
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过抛物线y2=4x的焦点F的直线l与椭圆C交于不同两点M，N，且满足$\overrightarrow{OM}$⊥$\overrightarrow{ON}$，求直线l的方程．
2．已知复数z=2+3i，则|z|=$\sqrt{13}$．
12．已知函数f（x）=$\frac{1}{3}$x3-ax2+（a2-1）x+b（a，b∈R）
（1）若x=1为f（x）的极值点，求a的值；
（2）若y=f（x）的图象在点（1，f（1））处的切线方程为x+y-3=0，求f（x）在区间[-2，4]上的最大值与最小值．
4．已知a＞c＞1＞b＞0，则（　　）
A．b-a＜b-cB．logab＞logcbC．ab+cb＜（a+c）bD．loga（c-b）＞logc（a-b）
1．已知不等式|2x-a|≤3的解集为[-1，2]．
（Ⅰ）求a的值；
（Ⅱ）若|x-m|＜a，求证：|x|＜|m|+1．
2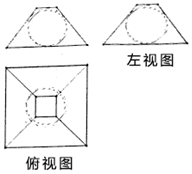．如图是某几何体挖去一部分后得到的三视图，其中主视图和左视图相同都是一个等腰梯形及它的内切圆，俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心．问该几何体的体积是（　　）
A．$\frac{420-32π}{3}$B．$\frac{336-32π}{3}$C．$\frac{168-4π}{3}$D．$\frac{168\sqrt{2}-64\sqrt{2}π}{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网