题目内容
1.已知不等式|2x-a|≤3的解集为[-1,2].(Ⅰ)求a的值;
(Ⅱ)若|x-m|<a,求证:|x|<|m|+1.
分析 (Ⅰ)利用绝对值不等式,求出解集,然后列出方程组求解即可.
(Ⅱ)利用第一问的结论,转化证明不等式即可.
解答 (Ⅰ)解:由不等式|2x-a|≤3可化为-3≤2x-a≤3,所以$\frac{a-3}{2}≤x≤\frac{a+3}{2}$,
不等式|2x-a|≤3的解集为[-1,2].
∴$\left\{{\begin{array}{l}{\frac{a-3}{2}=-1}\\{\frac{a+3}{2}=2}\end{array}}\right.得a=1$.
(Ⅱ)证明:由(Ⅰ)可得|x-m|<1,
|x|=|x-m+m|≤|x-m|+|m|<|m|+1.
所以:|x|<|m|+1.
点评 本题考查不等式的解法与证明,考查转化思想以及计算能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
6.已知集合M={1,2,3,4,5},集合N={x|log4x≥1},则M∩N=( )
| A. | {1,2,3} | B. | {4,5} | C. | N | D. | M |
7..函数y=2sinxcosx的导数为( )
| A. | y′=cosx | B. | y′=2cos2x | C. | y′=2(sin2x-cos2x) | D. | y′=-sin2x |
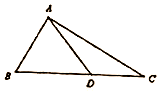 如图,在D是直角△ABC斜边BC上一点,$AC=\sqrt{3}DC$.
如图,在D是直角△ABC斜边BC上一点,$AC=\sqrt{3}DC$.