题目内容
已知两个集合A={x|
<0},B={x|log
x>1};命题p:实数m为小于6的正整数,命题q:A是B成立的必要不充分条件,若命题p∧q是真命题,求实数m的值.
| mx-1 |
| x |
| 1 |
| 2 |
考点:复合命题的真假
专题:简易逻辑
分析:本题的关键是求解不等式两个集合A={x|
<0},B={x|log
x>1};再给出命题P:实数m为小于6的正整数,命题q:A是B成立的必要不充分条件为真时m的取值范围,最后复合命题的真假判定p真q真给出m取值范围
| mx-1 |
| x |
| 1 |
| 2 |
解答:
解:∵命题p:实数m为小于6的正整数
∴A={x|
<0}={x|0<x<
}
∵B={x|log
x>1}
∴B={x|log
x>1}={x<0<
}
∴若p真,那么0<m<6,m∈N+
∵命题q:A是B成立的必要不充分条件
∴B?A,即
>
∵命题p∧q是真命题,
∴命题p和q都是真命题
实数m的值:m=1
∴A={x|
| mx-1 |
| x |
| 1 |
| m |
∵B={x|log
| 1 |
| 2 |
∴B={x|log
| 1 |
| 2 |
| 1 |
| 2 |
∴若p真,那么0<m<6,m∈N+
∵命题q:A是B成立的必要不充分条件
∴B?A,即
| 1 |
| m |
| 1 |
| 2 |
∵命题p∧q是真命题,
∴命题p和q都是真命题
实数m的值:m=1
点评:本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.

练习册系列答案
相关题目
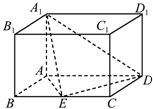 如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=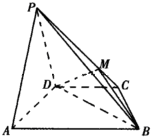 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8, 如图,已知线段AB、BD在平面α内,BD⊥AB,线段AC⊥α,如果AB=2,BD=5,AC=4,则C、D间的距离为
如图,已知线段AB、BD在平面α内,BD⊥AB,线段AC⊥α,如果AB=2,BD=5,AC=4,则C、D间的距离为
 (几何证明选讲选做题) 如图,∠ACB=90°,AC是圆O的切线,切点为E,割线ADB过圆心O,若
(几何证明选讲选做题) 如图,∠ACB=90°,AC是圆O的切线,切点为E,割线ADB过圆心O,若