题目内容
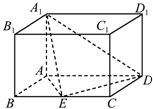 如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=| 2 |
(Ⅰ)证明:DE⊥平面A1AE;
(Ⅱ)求点A到平面A1ED的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:计算题,解题方法,空间位置关系与距离
分析:(Ⅰ)欲证DE⊥平面A1AE,根据线面垂直的判定定理可知只需证AE⊥DE,A1A⊥DE,即可;
(Ⅱ)利用第一问的结果,推出平面AA1E⊥平面A1ED,作出垂线,求解即可.
(Ⅱ)利用第一问的结果,推出平面AA1E⊥平面A1ED,作出垂线,求解即可.
解答:
证明:(Ⅰ)长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
,在△AED中,AE=DE=
,AD=2,
∴AE⊥DE.
∵A1A⊥平面ABCD,
∴A1A⊥DE,
∴DE⊥平面A1AE.
(Ⅱ)由DE⊥平面A1AE,∴平面AA1E⊥平面A1ED,
过A作AM⊥A1E,交A1E于M,由平面与平面垂直的性质定理可知,AM⊥平面A1ED,
AM就是A到平面A1ED的距离,在△AA1E中,AE=
,AA1=
,AE⊥AA1,
∴AM=1.
点A到平面A1ED的距离为:1.
| 2 |
| 2 |
∴AE⊥DE.

∵A1A⊥平面ABCD,
∴A1A⊥DE,
∴DE⊥平面A1AE.
(Ⅱ)由DE⊥平面A1AE,∴平面AA1E⊥平面A1ED,
过A作AM⊥A1E,交A1E于M,由平面与平面垂直的性质定理可知,AM⊥平面A1ED,
AM就是A到平面A1ED的距离,在△AA1E中,AE=
| 2 |
| 2 |
∴AM=1.
点A到平面A1ED的距离为:1.
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面垂直的判定,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,