题目内容
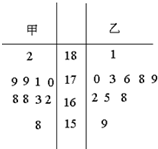随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．则两个班的样本中位数之和是（ ）| A、341 | B、341.5 |
| C、340 | D、340.5 |
考点：茎叶图
专题：
分析：利用茎叶图性质和中位数定义求解．
解答：
解：甲班同学中位数x甲=
=169，
乙班同学中位数x乙=
=171.5，
∴两个班的样本中位数之和为：
171.5+169=340.5．
故选：D．
| 168+170 |
| 2 |
乙班同学中位数x乙=
| 170+173 |
| 2 |
∴两个班的样本中位数之和为：
171.5+169=340.5．
故选：D．
点评：本题考查两个班的样本中位数的求法，是基础题，解题时要认真审题，注意茎叶图的合理运用．
练习册系列答案
相关题目
化简：
=（ ）
| 1-2sin2cos2 |
| A、sin2+cos2 |
| B、-（sin2+cos2） |
| C、sin2-cos2 |
| D、cos2-sin2 |
若复数2-bi（b∈R）的实部与虚部互为相反数，则b的值为（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
以下四个命题中，正确的是（ ）
A、向量
| ||||||||||||||||||
B、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
C、|（
| ||||||||||||||||||
D、若{
|
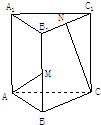如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，M、N分别是BB1和B1C1的中点，则直线AM与CN所成角的余弦值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等比数列{an}中，|a2|=2，a2014=-8a2011，a4＜a1，则an=（ ）
| A、-（-2）n |
| B、-（-2）n-1 |
| C、（-2）n |
| D、（-2）n-1 |
若定义在R上奇函数f（x）满足f（x）=f（x+5），且f（1）=1，f（2）=2，则f（3）-f（4）=（ ）
| A、-1 | B、1 | C、-2 | D、2 |