题目内容
等比数列{an}中，|a2|=2，a2014=-8a2011，a4＜a1，则an=（ ）
| A、-（-2）n |
| B、-（-2）n-1 |
| C、（-2）n |
| D、（-2）n-1 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由a2014=-8a2011可得q，再由其余条件可得a2，可得an
解答：
解：∵a2014=-8a2011，
∴q2014-2011=-8，解得q=-2，
由|a2|=2，可得a2=2或a2=-2，
∵a4＜a1，∴a2q2＜
，
∴a2=-2，∴an=（-2）n-1．
故选：D
∴q2014-2011=-8，解得q=-2，
由|a2|=2，可得a2=2或a2=-2，
∵a4＜a1，∴a2q2＜
| a2 |
| q |
∴a2=-2，∴an=（-2）n-1．
故选：D
点评：本题考查等比数列得性质，属基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
若平面α与平面β相交，直线a在α内，则直线a与β的位置关系是（ ）
| A、a在β内 |
| B、a在β外 |
| C、a与β平行或相交 |
| D、a与β平行或相交或a在β内 |
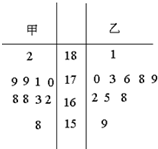随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．则两个班的样本中位数之和是（ ）| A、341 | B、341.5 |
| C、340 | D、340.5 |
已知i为虚数单位，则|
|=（ ）
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
log
sin
π+log
cos
π的值是（ ）
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
| A、4 | B、1 | C、-4 | D、-1 |
不等式x2+2x-3≤0的解是（ ）
| A、（-∞，-3] |
| B、[1，+∞） |
| C、[-3，1] |
| D、（-∞，-3]∪[1，+∞） |
已知点A（3，4，0）和向量
=（1，-2，1），点B（0，m，n）在yOz平面上，使向量
∥
，则点B的坐标为（ ）
| a |
| AB |
| a |
| A、（0，-10，3） |
| B、（0，10，-3） |
| C、（0，-2，3） |
| D、（0，2，-3） |