题目内容
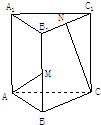 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M、N分别是BB1和B1C1的中点,则直线AM与CN所成角的余弦值等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以A为原点,在平面ABC处以过点A垂直于AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,利用向量法能求出直线AM与CN所成角的余弦值.
解答:
解: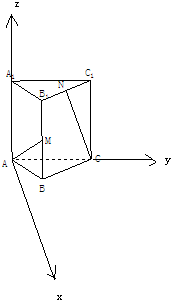 如图,以A为原点,在平面ABC处以过点A垂直于AC的直线为x轴,
如图,以A为原点,在平面ABC处以过点A垂直于AC的直线为x轴,
以AC为y轴,以AA1为z轴,
建立空间直角坐标系,
由题意知A(0,0,0),M(
,1,1),
C(0,2,0),N(
,
,2),
∴
=(
,1,1),
=(
,-
,2),
设直线AM与CN所成角的大小为θ,
则cosθ=|cos<
,
>|
=|
|=
.
故选:D.
 如图,以A为原点,在平面ABC处以过点A垂直于AC的直线为x轴,
如图,以A为原点,在平面ABC处以过点A垂直于AC的直线为x轴,以AC为y轴,以AA1为z轴,
建立空间直角坐标系,
由题意知A(0,0,0),M(
| 3 |
C(0,2,0),N(
| ||
| 2 |
| 3 |
| 2 |
∴
| AM |
| 3 |
| CN |
| ||
| 2 |
| 1 |
| 2 |
设直线AM与CN所成角的大小为θ,
则cosθ=|cos<
| AM |
| CN |
=|
| ||||
|
| 3 |
| 5 |
故选:D.
点评:本题考查异面直线所成角的余弦值的求法,是基础题,解题时要注意向量法的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
设集合A={x|x+1≥0},集合B=|x|x≥0},则A∪B=( )
| A、∅ |
| B、[0,+∞) |
| C、[-1,+∞) |
| D、[1,+∞) |
用反证法证明命题“设x,y∈(0,1),求证:对于a,b∈R,必存在满足条件的x,y,使|xy-ax-by|≥
成立.”第一步的假设为( )
| 1 |
| 3 |
A、对任意x,y∈(0,1),|xy-ax-by|≥
| ||
B、对任意x,y∈(0,1),|xy-ax-by|<
| ||
C、存在x,y∈(0,1),使|xy-ax-by|<
| ||
D、存在x,y∉(0,1),使|xy-ax-by|≥
|
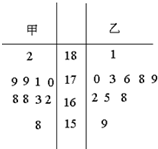 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )| A、341 | B、341.5 |
| C、340 | D、340.5 |
过点P(a,5)作圆(x+2)2+(y-1)2=4的切线,切线长为2
,则a等于( )
| 3 |
| A、-1 | B、-2 | C、-3 | D、0 |
log
sin
π+log
cos
π的值是( )
| 2 |
| 5 |
| 12 |
| 2 |
| 5 |
| 12 |
| A、4 | B、1 | C、-4 | D、-1 |
甲船在早6点至12点之间的任意时刻出发,则它早于8点出发的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
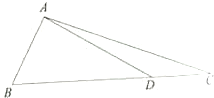 如图,△ABC中,D在边BC上,BD=2,CD=1,AD=
如图,△ABC中,D在边BC上,BD=2,CD=1,AD=