题目内容
化简：
=（ ）
| 1-2sin2cos2 |
| A、sin2+cos2 |
| B、-（sin2+cos2） |
| C、sin2-cos2 |
| D、cos2-sin2 |
考点：同角三角函数基本关系的运用,三角函数值的符号
专题：三角函数的求值
分析：由2的范围确定出sin2-cos2的正负，原式被开方数利用同角三角函数间基本关系及完全平方公式变形后，利用二次根式的性质及绝对值的代数意义化简即可得到结果．
解答：
解：∵
＜2＜π，
∴sin2＞0，cos2＜0，即sin2-cos2＞0，
原式=
=|sin2-cos2|=sin2-cos2．
故选：C．
| π |
| 2 |
∴sin2＞0，cos2＜0，即sin2-cos2＞0，
原式=
| (sin2-cos2)2 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，以及三角函数值的符号，熟练掌握基本关系是解本题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
设ξ是一个离散型随机变量，其分布列为
则ξ的期望为（ ）
| ξ | -1 | 0 | 1 | ||
| P |
|
1-2q | q2 |
A、
| ||||
B、1+
| ||||
C、1-
| ||||
D、1+
|
若抛物线的焦点是双曲线
-
=1的一个焦点，顶点是坐标原点，则抛物线的标准方程是（ ）
| y2 |
| 5 |
| x2 |
| 4 |
| A、y2=±4x |
| B、y2=12x |
| C、x2=±12y |
| D、x2=12y |
设集合A={x|x+1≥0}，集合B=|x|x≥0}，则A∪B=（ ）
| A、∅ |
| B、[0，+∞） |
| C、[-1，+∞） |
| D、[1，+∞） |
若平面α与平面β相交，直线a在α内，则直线a与β的位置关系是（ ）
| A、a在β内 |
| B、a在β外 |
| C、a与β平行或相交 |
| D、a与β平行或相交或a在β内 |
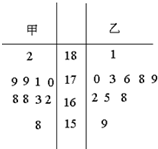随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．则两个班的样本中位数之和是（ ）| A、341 | B、341.5 |
| C、340 | D、340.5 |
已知点A（3，4，0）和向量
=（1，-2，1），点B（0，m，n）在yOz平面上，使向量
∥
，则点B的坐标为（ ）
| a |
| AB |
| a |
| A、（0，-10，3） |
| B、（0，10，-3） |
| C、（0，-2，3） |
| D、（0，2，-3） |