题目内容
以下四个命题中,正确的是( )
A、向量
| ||||||||||||||||||
B、△ABC为直角三角形的充要条件是
| ||||||||||||||||||
C、|(
| ||||||||||||||||||
D、若{
|
考点:命题的真假判断与应用
专题:空间向量及应用,简易逻辑
分析:A.利用向量共线定理即可判断出;
B.△ABC为直角三角形,若A≠
,则推不出
•
=0;
C.|(
•
)
|=|
| |
||
|cos<
,
>≠|
| |
||
|;
D.利用向量共面定理即可判断出.
B.△ABC为直角三角形,若A≠
| π |
| 2 |
| AB |
| AC |
C.|(
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
D.利用向量共面定理即可判断出.
解答:
解:A.设
=(1,-1,3)与向量
=(3,-3,6)平行,则存在实数λ使得
=λ
,则
,此方程组无解,因此
与
不共线,故不正确.
B.△ABC为直角三角形,若A≠
,则推不出
•
=0,因此不正确;
C.|(
•
)
|=|
| |
||
|cos<
,
>≠|
| |
||
|,因此不正确;
D.假设存在不全为0的实数λ,μ使得
+
=λ(
+
)+μ(
+
),化为(1-μ)
+(1-λ)
+(-λ-μ)
=
,
∵{
,
,
}为空间的一个基底,∴
,此方程组无解,因此
+
,
+
,
+
是不共面向量,可构成空间的另一个基底.
综上可知:只有D正确.
故选:D.
| a |
| b |
| a |
| b |
|
| a |
| b |
B.△ABC为直角三角形,若A≠
| π |
| 2 |
| AB |
| AC |
C.|(
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
D.假设存在不全为0的实数λ,μ使得
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| c |
| 0 |
∵{
| a |
| b |
| c |
|
| a |
| b |
| b |
| c |
| c |
| a |
综上可知:只有D正确.
故选:D.
点评:本题考查了向量共线定理、向量垂直于数量积的关系、数量积运算、向量共面定理等基础知识,考查了推理能力,属于中档题.

练习册系列答案
相关题目
若抛物线的焦点是双曲线
-
=1的一个焦点,顶点是坐标原点,则抛物线的标准方程是( )
| y2 |
| 5 |
| x2 |
| 4 |
| A、y2=±4x |
| B、y2=12x |
| C、x2=±12y |
| D、x2=12y |
若平面α与平面β相交,直线a在α内,则直线a与β的位置关系是( )
| A、a在β内 |
| B、a在β外 |
| C、a与β平行或相交 |
| D、a与β平行或相交或a在β内 |
sin780°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
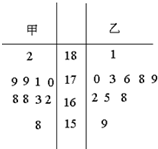 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )| A、341 | B、341.5 |
| C、340 | D、340.5 |
已知i为虚数单位,则|
|=( )
| 1+i |
| i |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
不等式x2+2x-3≤0的解是( )
| A、(-∞,-3] |
| B、[1,+∞) |
| C、[-3,1] |
| D、(-∞,-3]∪[1,+∞) |