题目内容
(1)解不等式|x-1|+|x+2|≥5;
(2)求函数f(x)=|x-1|+|x+2|的最小值.
(2)求函数f(x)=|x-1|+|x+2|的最小值.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)通过对x取值范围的分类讨论,去掉绝对值符号后解相应的一次不等式即可求得其解集;
(2)利用绝对值不等式的几何意义f(x)=|x-1|+|x+2|≥|(x-1)-(x+2)|=3即可求得函数f(x)=|x-1|+|x+2|的最小值.
(2)利用绝对值不等式的几何意义f(x)=|x-1|+|x+2|≥|(x-1)-(x+2)|=3即可求得函数f(x)=|x-1|+|x+2|的最小值.
解答:
解:(1)当x<-2时,由1-x+(-x-2)≥5得x≤-3;
当-2≤x≤1时,|x-1|+|x+2|=1-x+x+2=3≥5的解集为∅;
当x>1时,|x-1|+|x+2|=x-1+x+2=2x+1≥5,得x≥2;
∴不等式|x-1|+|x+2|≥5的解集为{x|x≤-3或x≥2};
(2)∵f(x)=|x-1|+|x+2|≥|(x-1)-(x+2)|=3,
∴f(x)=|x-1|+|x+2|的最小值为3.
当-2≤x≤1时,|x-1|+|x+2|=1-x+x+2=3≥5的解集为∅;
当x>1时,|x-1|+|x+2|=x-1+x+2=2x+1≥5,得x≥2;
∴不等式|x-1|+|x+2|≥5的解集为{x|x≤-3或x≥2};
(2)∵f(x)=|x-1|+|x+2|≥|(x-1)-(x+2)|=3,
∴f(x)=|x-1|+|x+2|的最小值为3.
点评:本题考查绝对值不等式的解法,通过对x取值范围的分类讨论,去掉绝对值符号是关键,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
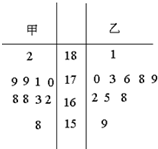 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.则两个班的样本中位数之和是( )| A、341 | B、341.5 |
| C、340 | D、340.5 |
已知点A(3,4,0)和向量
=(1,-2,1),点B(0,m,n)在yOz平面上,使向量
∥
,则点B的坐标为( )
| a |
| AB |
| a |
| A、(0,-10,3) |
| B、(0,10,-3) |
| C、(0,-2,3) |
| D、(0,2,-3) |
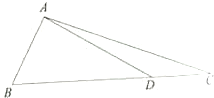 如图,△ABC中,D在边BC上,BD=2,CD=1,AD=
如图,△ABC中,D在边BC上,BD=2,CD=1,AD=