题目内容

计算
∫
0
-π
（cosx+ex）dx=
 
．
考点：定积分
专题：导数的概念及应用
分析：根据微积分基本定理计算即可．
解答： 解：
∫
0
-π
（cosx+ex）dx=（sinx+ex）
|
0
-π
=sin0+e0-（sin（-π）+e-π）=1-
1
eπ

故答案为：1-
1
eπ
点评：本题主要考查了定积分的计算，关键是求出原函数，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=ex-ax-1（a∈R）．
（1）讨论f（x）=ex-ax-1（a∈R）的单调性；
（2）若a=1，求证：当x≥0时，f（x）≥f（-x）．
已知在等比数列{an}中，若m+2n+p=s+2t+r，m，n，p，s，t，r∈N*，则am•an2•ap=as•at2•ar．类比此结论，可得到等差数列{bn}的一个正确命题，该命题为：在等差数列{bn}中，若m+2n+p=s+2t+r，m，n，p，s，t，r∈N*，则
 
．
已知
a
+
b
+
c
=
0
，且|
a
|=3，|
b
|=4，|
c
|=5，则
a
•
b
+
b
•
c
+
c
•
a
=
 
，
a
•
b
=
 
．
在空间直角坐标系中，M（1，2，3），N（2，3，4），则|MN|=
 
．
已知样本数据{x1，x2，…，xn}的方差为a，则样本数据{2x1+1，2x2+1，…，2xn+1}的方差为
 
．
不等式x2+3＜4x的解集为
 
．
设ξ是一个离散型随机变量，其分布列为
ξ -1 0 1
P
1
2
 1-2q q2
则ξ的期望为（　　）
A、
1
2
B、1+
2
C、1-
2
D、1+
2
或1-
2
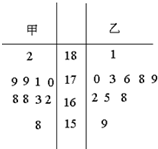随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图．则两个班的样本中位数之和是（　　）
A、341B、341.5
C、340D、340.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网