题目内容
 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.(1)求证:直线AE∥平面PCD;
(2)求平面PCD与平面PAB所成角的正弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)取PC的中点F,连接EF、DF,由已知条件推导出EF平行且等于
BC,从而得到四边形AEFD为平行四边形,由此能证明AE∥平面PCD.
(2)取AB的中点O,CD的中点Q,连接OP,OQ.以O为坐标原点,分别以OP、OB、OQ为x、y、z轴建立空间直角坐标系,利用向量法能求出平面PCD与平面PAB所成角的正弦值.
| 1 |
| 2 |
(2)取AB的中点O,CD的中点Q,连接OP,OQ.以O为坐标原点,分别以OP、OB、OQ为x、y、z轴建立空间直角坐标系,利用向量法能求出平面PCD与平面PAB所成角的正弦值.
解答:
(1)证明:如图1取PC的中点F,连接EF、DF.
在△PBC中,PE=EB,PF=FC,
所以EF平行且等于
BC,
又AD平行且等于
BC,
所以EF平行且等于AD,故四边形AEFD为平行四边形,
所以AE∥DF,
又因为AE?面PCD,DF?面PCD,
所以AE∥平面PCD.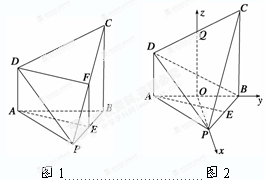
(2)解:如图2,取AB的中点O,CD的中点Q,连接OP,OQ.
在△APB中,AP=PB,OA=OB,∠APB=90°,
所以PO⊥AB,且PO=
AB=1.
在直角梯形ABCD中,AO=OB,DQ=QC,
所以OQ∥BC,
又因为BC⊥AB,所以OQ⊥AB,
又因为面APB⊥面ABCD,面APB∩面ABCD=AB,
所以OQ⊥面PAB.
以O为坐标原点,分别以OP、OB、OQ为x、y、z轴建立空间直角坐标系,
则P(1,0,0),A(0,-1,0),B(0,1,0),C(0,1,2),D(0,-1,1).
故
=(-1,-1,1),
=(-1,1,2).
设面PCD的法向量为n=(x,y,z),
则由
,
令y=1,则z=-2,x=-3.
故n=(-3,1,-2)为面PCD的一个法向量.
因为OQ⊥面PAB,所以可取m=(0,0,1)为面PAB的一个法向量.
故cos<m,n>=
=
=-
.
设所求二面角为θ,所以|cos θ|=|cos<m,n>|=
,
所以sinθ=
=
.
在△PBC中,PE=EB,PF=FC,
所以EF平行且等于
| 1 |
| 2 |
又AD平行且等于
| 1 |
| 2 |
所以EF平行且等于AD,故四边形AEFD为平行四边形,
所以AE∥DF,
又因为AE?面PCD,DF?面PCD,
所以AE∥平面PCD.

(2)解:如图2,取AB的中点O,CD的中点Q,连接OP,OQ.
在△APB中,AP=PB,OA=OB,∠APB=90°,
所以PO⊥AB,且PO=
| 1 |
| 2 |
在直角梯形ABCD中,AO=OB,DQ=QC,
所以OQ∥BC,
又因为BC⊥AB,所以OQ⊥AB,
又因为面APB⊥面ABCD,面APB∩面ABCD=AB,
所以OQ⊥面PAB.
以O为坐标原点,分别以OP、OB、OQ为x、y、z轴建立空间直角坐标系,
则P(1,0,0),A(0,-1,0),B(0,1,0),C(0,1,2),D(0,-1,1).
故
| PD |
| PC |
设面PCD的法向量为n=(x,y,z),
则由
|
令y=1,则z=-2,x=-3.
故n=(-3,1,-2)为面PCD的一个法向量.
因为OQ⊥面PAB,所以可取m=(0,0,1)为面PAB的一个法向量.
故cos<m,n>=
| m•n |
| |m||n| |
| -2 | ||
|
| ||
| 7 |
设所求二面角为θ,所以|cos θ|=|cos<m,n>|=
| ||
| 7 |
所以sinθ=
1-(
|
| ||
| 7 |
点评:本题考查查直线与平面平行的证明,考查二面角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象的相邻两对称中心的距离为π,且f(x+
)=f(-x),则函数y=f(
-x)是( )
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| A、偶函数且在x=0处取得最大值 |
| B、偶函数且在x=0处取得最小值 |
| C、奇函数且在x=0处取得最大值 |
| D、奇函数且在x=0处取得最小值 |