题目内容
在等差数列{an}中,a3=5,a2+2a5=21.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Sn=a1+a2+a3+…+an,若S3,Sk,S12成等比数列,求k的值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Sn=a1+a2+a3+…+an,若S3,Sk,S12成等比数列,求k的值.
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:(I)设等差数列{an}的公差为d,可得首项和公差的方程组,解方程组可得通项公式;(II)由(I)可得Sn=n2,由S3,Sk,S12成等比数列可得k的方程,解方程可得.
解答:
解:(I)设等差数列{an}的公差为d,
则
,
解方程组可得a1=1,d=2
∴an=1+2(n-1)=2n-1
(II)由(I)Sn=a1+a2+a3+…+an=
=n2,
∵S3,Sk,S12成等比数列,
∴Sk2=S3•S12,即(k2)2=32×122,解得k=6
则
|
解方程组可得a1=1,d=2
∴an=1+2(n-1)=2n-1
(II)由(I)Sn=a1+a2+a3+…+an=
| n(1+2n-1) |
| 2 |
∵S3,Sk,S12成等比数列,
∴Sk2=S3•S12,即(k2)2=32×122,解得k=6
点评:本题考查等差数列,涉及通项公式和求和公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合M={y|y=2sinx,-2≤x≤2},N={x|lgx>0},则M∩N=( )
| A、{x|1<x≤5} |
| B、{x|-1<x≤0} |
| C、{x|-2<x≤0} |
| D、{x|1<x≤2} |
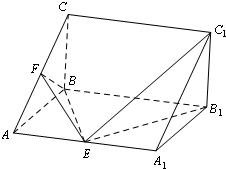 如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=
如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC= 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.