题目内容
A，B，C是△ABC的三个内角，下面说法：①至多有一个角大于60°；②至少有两个角大于或等于60°；③至少有一个角小于60°；④至多有两个角小于60°．其中正确的个数是（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：命题的真假判断与应用
专题：阅读型
分析：通过举反例，来判断①、②、③的正误；假设三角形的三个内角都小于60°，则内角和小于180°，与内角和定理矛盾，故不成立，举出两个角小于60°的情况，即可判断④．
解答：
解：①比如A=B=80°，C=20°，故①错；
②比如钝角△ABC中，A=120°，B=C=30°，只有一个角大于60°，故②错；
③比如等边三角形，所有内角均为60°，故③错；
④假设有三个内角均小于60°，则内角和小于180°，不成立，故不可能，比如A=150°，B=C=15°，则有两个角小于60°，故④正确．
故正确的个数为1．
故选C．
②比如钝角△ABC中，A=120°，B=C=30°，只有一个角大于60°，故②错；
③比如等边三角形，所有内角均为60°，故③错；
④假设有三个内角均小于60°，则内角和小于180°，不成立，故不可能，比如A=150°，B=C=15°，则有两个角小于60°，故④正确．
故正确的个数为1．
故选C．
点评：本题以命题的真假判断为载体，考查三角形的三个内角与60°的大小关系，考查逻辑推理能力，是一道基础题．
练习册系列答案
相关题目
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直，AD∥BC，∠APB=∠ABC=90°，AB=BC=2AD=2，E为PB的中点．设集合M={y|y=2sinx，-2≤x≤2}，N={x|lgx＞0}，则M∩N=（ ）
| A、{x|1＜x≤5} |
| B、{x|-1＜x≤0} |
| C、{x|-2＜x≤0} |
| D、{x|1＜x≤2} |
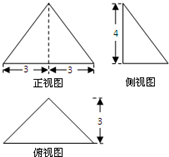如图是某个四面体的三视图，若在该四面体的外接球内任取一点，则点落在四面体内的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
的值域为（ ）
| 2sinx-3 |
| sinx-1 |
| A、（-∞，-2] | ||
B、（-∞，
| ||
| C、（-2，+∞） | ||
D、[
|
函数f（x）的定义域为R，f（-1）=1，对任意x∈R，f′（x）＞3，则f（x）＞3x+4的解集为（ ）
| A、（-1，1） |
| B、（-1，+∞） |
| C、（-∞，-1） |
| D、（-∞，+∞） |
已知集合M={x∈Z|log3x≤1}，N={x∈Z|x2-2x＜0}，则（ ）
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、M?N |
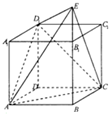如图长方体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形，E为BB1延长线上的一点且满足