Question

在约束条件

x≥1 y≥0 2x+y≤a

下，设目标函数z=x+y的最大值为M，则当4≤a≤6时，M的取值范围是（　　）

• A、[3，5]
• B、[2，4]
• C、[1，4]
• D、[2，5]

Answer 1

考点：简单线性规划

专题：数形结合

分析：由约束条件作出可行域，化目标函数z=x+y为直线方程的斜截式y=-x+z，可知当直线在y轴上的截距最大时z最大，结合图象找出满足条件的点，联立直线方程求出点的坐标，代入目标函数，然后结合a得范围得答案．

解答： 解：∵4≤a≤6，
∴由约束条件

x≥1 y≥0 2x+y≤a

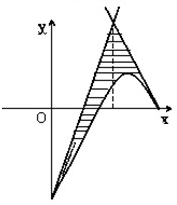
作可行域如图，
由z=x+y，得y=-x+z，
∴当直线y=-x+z过可行域内的点C时直线在y轴上的截距最大，z最大．
联立

x=1 2x+y=a

，解得

x=1 y=a-2

．
∴C（1，a-2）．
则目标函数z=x+y的最大值为M=1+a-2=a-1．
∵4≤a≤6，
∴M∈[3，5]．
故选：A．

点评：本题考查了简单的线性规划，训练了数形结合的解题思想方法，关键是正确作出可行域，是中档题．