题目内容
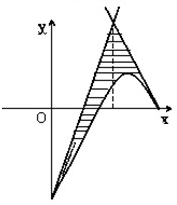
求由抛物线y=-x2+4x-3与它在点A（0，-3）和点B（3，0）的切线所围成的区域面积．
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：求出函数的切线方程，利用积分的几何意义即可求出区域的面积．
解答：
解：∵y=-x2+4x-3，
∴y′=-2x+4，
x=0时，y′=4，x=3时，y′=-2，
∴在点A（0，-3）和点B（3，0）的切线方程分别为y=4x-3和y=-2x+6，
两条切线的交点是（1.5，3），如图所示，区域被直线x=1.5分成了两部分，
∴所求面积为S=
[(4x-3)-(-x2+4x-3)]dx+
[(-2x+6)-(-x2+4x-3)]dx
=
x3
+(
x3-3x2+9x)
=2.25．
解：∵y=-x2+4x-3，∴y′=-2x+4，
x=0时，y′=4，x=3时，y′=-2，
∴在点A（0，-3）和点B（3，0）的切线方程分别为y=4x-3和y=-2x+6，
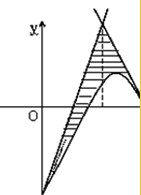
两条切线的交点是（1.5，3），如图所示，区域被直线x=1.5分成了两部分，
∴所求面积为S=
| ∫ | 1.5 0 |
| ∫ | 3 1.5 |
=
| 1 |
| 3 |
| | | 1.5 0 |
| 1 |
| 3 |
| | | 3 1.5 |
点评：本题主要考查导数的应用，利用导数的几何意义求出切线方程，以及利用积分求区域面积是解决本题的关键．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
已知a∈{2，3}，b∈{1，2，3}，执行如图所示程序框图，则输出的结果共有（ ）
| A、3种 | B、4种 | C、5种 | D、6种 |
在约束条件
下，设目标函数z=x+y的最大值为M，则当4≤a≤6时，M的取值范围是（ ）
|
| A、[3，5] |
| B、[2，4] |
| C、[1，4] |
| D、[2，5] |