题目内容
2.函数y=x-$\frac{4}{x}$的零点个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
分析 利用函数的零点与方程根的关系,求出解,即可得到根的个数.
解答 解:函数y=x-$\frac{4}{x}$的零点个数是方程x-$\frac{4}{x}$=0的解的个数,
可得x2-4=0,解得x=±2.
所以函数的零点有2个.
故选:C.
点评 本题考查函数的零点个数,考查计算能力,是基础题.

练习册系列答案
相关题目
10.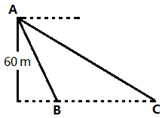 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )| A. | $30\sqrt{3}$ | B. | $30({\sqrt{3}-1})$ | C. | $40\sqrt{3}$ | D. | $40({\sqrt{3}-1})$ |
17.已知函数$f(x)=sin(\frac{1}{4}x+\frac{π}{6})\;(x∈R)$,把函数f(x)的图象向右平移$\frac{8π}{3}$个单位得函数g(x)的图象,则下面结论正确的是( )
| A. | 函数g(x)是奇函数 | B. | 函数g(x)在区间[π,2π]上是增函数 | ||
| C. | 函数g(x)的最小正周期是4π | D. | 函数g(x)的图象关于直线x=π对称 |
7.若ab>0,则a|a|>b|b|是a>b的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.设向量$\overrightarrow{a}$=(1,7),$\overrightarrow{b}$=(-3,4),则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | 5$\sqrt{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | 5 | D. | -5 |
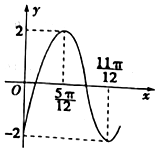 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.