Question

已知函数f（x）是定义在R上的奇函数，它的图象关于直线x=1对称，且f（x）=x（0＜x≤1）．若函数y=f（x）-

1

x

-a在区间[-10，10]上有10个零点（互不相同），则实数a的取值范围是（　　）

• A、[-

  4

  5

  ，

  4

  5

  ]
• B、（-

  4

  5

  ，

  4

  5

  ）
• C、[-

  1

  10

  ，

  1

  10

  ]
• D、（-

  1

  10

  ，

  1

  10

  ）

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：根据f（x）的图象关于x=1对称得f（1+x）=f（1-x），由f（x）是R上的奇函数求出函数的周期，再画出f（x）和y=

1

x

的图象（第一象限部分），由图得函数y=f（x）-

1

x

-a在区间[-10，10]上有10个零点的条件，列出不等式组求出实数a的取值范围．

解答： 解：因为f（x）的图象关于x=1对称，所以f（1+x）=f（1-x）
因为f（x）是R上的奇函数，所以f（x+1）=-f（x-1）．
所以f（x+2）=-f（x），f（x+4）=-f（x+2）=f（x）．
则f（x）是周期为4的函数，
由f（x）=x（0＜x≤1）画出f（x）和y=

1

x

的图象（第一象限部分）：
．
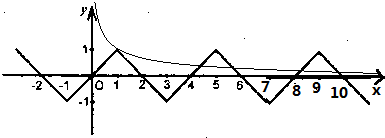因为函数y=f（x）-

1

x

-a在区间[-10，10]上有10个零点，
所以y=f（x）与y=

1

x

+a在区间[-10，10]上有10个不同的交点，
因为y=f（x）与y=

1

x

是奇函数，所研究第一象限的部分交点问题即可，
而y=

1

x

+a的图象是由y=

1

x

的图象上下平移得到，
由图得，向上平移时保证图象第三象限的部分在x轴的下方，则第一象限的部分有4个交点，
第三象限的部分有6个交点，
同理向下平移时保证图象第一象限的部分在x轴的上方，则第一象限的部分有6个交点，
第三象限的部分有4个交点，
即

- 1 10 +a≤0 1 10 +a≥0

，解得-

1

10

≤a≤

1

10

，
故选：C．

点评：本题考查函数的周期性、奇偶性、对称性的综合应用，图象平移问题，以及反比列函数的图象，考查数形结合，数形结合是高考中常用的方法，属于难题．