题目内容
给出四个函数,分别满足①f(x+y)=f(x)+f(y);②g(x+y)=g(x)•g(y);③ϕ(x•y)=ϕ(x)+ϕ(y);④ω(x•y)=ω(x)•ω(y),又给出四个函数的图象如下:
则正确的配匹方案是( )

则正确的配匹方案是( )
| A、①-M ②-N ③-P ④-Q |
| B、①-N ②-P ③-M ④-Q |
| C、①-P ②-M ③-N ④-Q |
| D、①-Q ②-M ③-N ④-P |
考点:函数的图象
专题:函数的性质及应用
分析:本题考查的是函数的图象变化和函数的性质问题.在解答时,可以先对图象逐一进行常见基本初等函数的对应,再结合特殊情况下函数的特性进行性质的选择.问题即可获得解答.
解答:
解:对于图象Q,可以选择函数y=2x考虑,∴性质①符合;
对于图象M,可以选择函数y=2x,∴性质②符合;
对于图象N,可以选择函数 y=x2,∴性质④符合;
对于图象P,可以选择函数 y=lgx.∴性质③符合.
故选D.
对于图象M,可以选择函数y=2x,∴性质②符合;
对于图象N,可以选择函数 y=x2,∴性质④符合;
对于图象P,可以选择函数 y=lgx.∴性质③符合.
故选D.
点评:本题考查的是函数的图象变化和函数的性质问题.在解答的过程当中充分体现了观察图象、分析图象应用图象了能力,特殊到一般的思想以及常见基本初等函数性质的抽象应用.值得同学们体会反思.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,它的图象关于直线x=1对称,且f(x)=x(0<x≤1).若函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),则实数a的取值范围是( )
| 1 |
| x |
A、[-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-
|
已知函数f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么f(x+1)<1的解集的补集是( )
| A、(-1,2) |
| B、(1,4) |
| C、[2,+∞) |
| D、[4,+∞) |
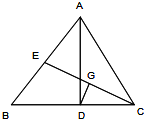 如图所示,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于G,EC的长为8,则EG=
如图所示,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于G,EC的长为8,则EG=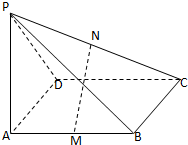 如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)
如图所示,ABCD是矩形,PA⊥平面ABCD,△PAD是等腰三角形,M、N分别是AB、PC的中点.求证:MN⊥平面PCD.(向量法证明)