题目内容
已知函数f（x）=9x-4•3x+5，x∈[0，2]，求函数f（x）的最大值与最小值．
考点：二次函数在闭区间上的最值
专题：计算题,函数的性质及应用
分析：令3x=t，则t∈[1，9]，所以f（x）=9x-4•3x+5可化为g（t）=t2-4t+5=（t-2）2+1．利用配方法求最值．
解答：
解：令3x=t，则t∈[1，9]，
所以f（x）=9x-4•3x+5可化为
g（t）=t2-4t+5=（t-2）2+1．
故当t=2时，f（x）有最小值g（2）=1；
当t=9时，f（x）有最大值g（9）=50．
所以f（x）=9x-4•3x+5可化为
g（t）=t2-4t+5=（t-2）2+1．
故当t=2时，f（x）有最小值g（2）=1；
当t=9时，f（x）有最大值g（9）=50．
点评：本题考查了换元法及配方法在求最值时的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）是定义在R上的奇函数，它的图象关于直线x=1对称，且f（x）=x（0＜x≤1）．若函数y=f（x）-
-a在区间[-10，10]上有10个零点（互不相同），则实数a的取值范围是（ ）
| 1 |
| x |
A、[-
| ||||
B、（-
| ||||
C、[-
| ||||
D、（-
|
已知函数f（x）是R上的增函数，A（0，-1），B（3，1）是其图象上的两点，那么f（x+1）＜1的解集的补集是（ ）
| A、（-1，2） |
| B、（1，4） |
| C、[2，+∞） |
| D、[4，+∞） |
设l，m是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（ ）
| A、若l⊥m，m=α∩β，则l⊥α |
| B、若l∥m，m=α∩β，则l∥α |
| C、若α∥β，l与α所成的角相等，则l∥m |
| D、若l∥m，l⊥α，α∥β，则m⊥β |
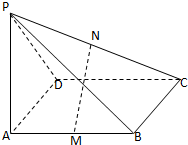如图所示，ABCD是矩形，PA⊥平面ABCD，△PAD是等腰三角形，M、N分别是AB、PC的中点．求证：MN⊥平面PCD．（向量法证明）