题目内容
设函数f(x)(x∈R)满足f(x+2)=2f(x)+x,且当0≤x<2时,f(x)=[x]([x]表示不超过x的最大整数),则f(5.5)=( )
| A、8.5 | B、10.5 |
| C、12.5 | D、14.5 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:此题类似于函数的周期性,应先将f(5.5)转化到区间[0,2]上来,然后取整求解.
解答:
解:由题意f(x+2)=2f(x)+x得:
f(5.5)=2f(3.5)+3.5=2[2f(1.5)+1.5]+3.5
=4f(1.5)+6.5
=4×1+6.5
=10.5.
故选B
f(5.5)=2f(3.5)+3.5=2[2f(1.5)+1.5]+3.5
=4f(1.5)+6.5
=4×1+6.5
=10.5.
故选B
点评:本题考查了抽象函数的性质,此题的关键在于利用条件“f(x+2)=2f(x)+x”实现将所求转化为已知.这是此类问题考查的主要解题思想.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,它的图象关于直线x=1对称,且f(x)=x(0<x≤1).若函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),则实数a的取值范围是( )
| 1 |
| x |
A、[-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-
|
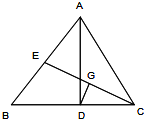 如图所示,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于G,EC的长为8,则EG=
如图所示,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于G,EC的长为8,则EG=