题目内容

已知f（x）=
a
•
b
-1，其中向量
a
=（
3
sin2x，cosx），
b
=（1，2cosx），x∈[0，
π
2
]，则f（x）的单调递减区间为
 
．
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：三角函数的图像与性质,平面向量及应用
分析：先根据数量积的坐标运算及两角和的正弦公式得出f（x）=2sin（2x+
π
6
），根据x的范围求出2x+
π
6
的范围，然后根据正弦函数以及复合函数的单调性即可求出f（x）的单调递减区间．
解答： 解：f（x）=
3
sin2x+2cos2x-1=
3
sin2x+cos2x=2sin(2x+
π
6
)；
∵x∈[0，
π
2
]，∴2x+
π
6
∈[
π
6
，
7π
6
]；
根据正弦函数的单调性及复合函数的单调性知：
2x+
π
6
∈[
π
2
，
7π
6
]，即x∈[
π
6
，
π
2
]时，f（x）单调递减；
∴f（x）的单调递减区间为[
π
6
，
π
2
]．
故答案为：[
π
6
，
π
2
]．
点评：考查向量数量积的坐标运算，两角和的正弦公式，正弦函数的单调性以及复合函数的单调性．
练习册系列答案
相关题目
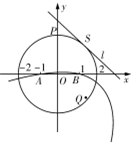如图，已知圆O：x2+y2=4与y轴正半轴交于点P，A（-1，0），B（1，0），直线l与圆O切于点S（l不垂直于x轴），抛物线过A、B两点且以l为准线．
（1）当点S在圆周上运动时，试求抛物线的焦点Q的轨迹方程；
（2）设M，N是（1）中的点Q的轨迹上除与y轴两个交点外的不同两点，且
PM
=t
PN
（t∈R），问：△MON（O为坐标原点）的面积是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．
已知实数x、y满足方程x2+y2-4x+1=0．
（1）求y-x的最大值和最小值；
（2）求x2+y2的最最大值和最小值．
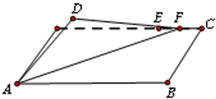如图，在长方形ABCD中，AB=4，BC=1，E为DC的四等分点（靠近C处），F为线段EC上一动点（包括端点），现将△AFD沿AF折起，使D点在平面内的射影恰好落在边AB上，则当F运动时，二面角D-AF-B的平面角余弦值的变化范围为
 
．
f（x）是偶函数，在[0，+∞）递增，f（x+1）=f（
x+1
x
）的所有实根之和．
设函数y=x2-2x+2的图象为C1，函数y=-x2+ax+b的图象为C2，已知过C1和C2的一个交点的两切线互相垂直
（1）求a，b之间的关系；
（2）求ab的最大值．
已知函数f（x）=logax的反函数的图象过点（4，4），则a=
 
．
两名高一年级的学生被允许参加高二年级的学生象棋比赛，每两名参赛选手之间都比赛一次，胜者得1分，和棋各得0.5分，输者得0分，即每场比赛双方的得分之和是1分．两名高一年级的学生共得8分，且每名高二年级的学生都得相同分数，则有
 
名高二年级的学生参加比赛．（结果用数值作答）
已知点P为椭圆
x2
4
+y2=1上的一点，F1，F2是椭圆的焦点，且∠F1PF2=
π
3
，则△F1PF2的面积为（　　）
A、
3
3
B、
3
C、2
D、
5
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网