题目内容
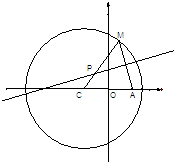 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P是线段AM的垂直平分线与直线CM的交点.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P是线段AM的垂直平分线与直线CM的交点.(1)求点P的轨迹曲线E的方程;
(2)设点P(x0,y0)是曲线E上任意一点,写出曲线E在点P(x0,y0)处的切线l的方程;(不要求证明)
(3)直线m过切点P(x0,y0)与直线l垂直,点C关于直线m的对称点为D,证明:直线PD恒过一定点,并求定点的坐标.
考点:圆的切线方程
专题:综合题,直线与圆
分析:(1)利用点P是线段AM的垂直平分线与直线CM的交点,可得PA=PM,从而可得PA+PC=PM+PC,利用椭圆的定义,即可求点P的轨迹曲线E的方程;
(2)曲线E在点P(x0,y0)处的切线l的方程是
+y0y=1;
(3)直线m的方程为x0(y-y0)=2y0(x-x0),即2y0x-x0y-x0y0=0.求出点C关于直线m的对称点D的坐标,确定直线PD的方程,化简即可得出结论.
(2)曲线E在点P(x0,y0)处的切线l的方程是
| x0x |
| 2 |
(3)直线m的方程为x0(y-y0)=2y0(x-x0),即2y0x-x0y-x0y0=0.求出点C关于直线m的对称点D的坐标,确定直线PD的方程,化简即可得出结论.
解答:
(1)解:∵点P是线段AM的垂直平分线与直线CM的交点,
∴PA=PM,
∴PA+PC=PM+PC=2
>AC=2,
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
椭圆长轴长为2a=2
,焦距2c=2,
∴a=
,c=1,b=1,
∴曲线E的方程为
+y2=1 …5′
(2)解:曲线E在点P(x0,y0)处的切线l的方程是
+y0y=1.…8′
(3)证明:直线m的方程为x0(y-y0)=2y0(x-x0),即2y0x-x0y-x0y0=0.
设点C关于直线m的对称点的坐标为D(m,n),
则
,解得
∴直线PD的斜率为k=
=
从而直线PD的方程为:y-y0=
(x-x0)
即x=
y+1,从而直线PD恒过定点A(1,0).…16′
∴PA=PM,
∴PA+PC=PM+PC=2
| 2 |
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
椭圆长轴长为2a=2
| 2 |
∴a=
| 2 |
∴曲线E的方程为
| x2 |
| 2 |
(2)解:曲线E在点P(x0,y0)处的切线l的方程是
| x0x |
| 2 |
(3)证明:直线m的方程为x0(y-y0)=2y0(x-x0),即2y0x-x0y-x0y0=0.
设点C关于直线m的对称点的坐标为D(m,n),
则
|
|
∴直线PD的斜率为k=
| n-y0 |
| m-x0 |
| x04+4x03+2x02-8x0-8 |
| 2y0(-x03-3x02+4) |
从而直线PD的方程为:y-y0=
| x04+4x03+2x02-8x0-8 |
| 2y0(-x03-3x02+4) |
即x=
| 2y0(-x03-3x02+4) |
| x04+4x03+2x02-8x0-8 |
点评:本题考查椭圆的定义与标准方程,考查与椭圆的位置关系,考查直线恒过定点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合M={x||x|<3},集合N={x|(x+4)(x-2)≤0},则M∩N=( )
| A、{x|-4<x≤3} |
| B、{x|-3<x≤2} |
| C、{x|-3<x<2} |
| D、{x|-4≤x≤2} |
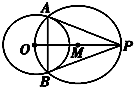 如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.
如图,已知P为⊙O外一点,以PO为直径作⊙M,⊙M交⊙O于A、B两点,求证:PA、PB是⊙O的切线.