题目内容
已知直线l的斜率为2，且直线过（-1，3）点，求直线l与坐标轴的交点坐标．
考点：直线的点斜式方程
专题：直线与圆
分析：由于直线l的斜率为2，且直线过（-1，3）点，利用点斜式即可得到可得直线l的方程．分别令x=0，y=0，即可得到直线l与坐标轴的交点坐标．
解答：
解：∵直线l的斜率为2，且直线过（-1，3）点，
∴直线l的方程为：y-3=2（x+1），化为2x-y+5=0．
令x=0，得到y=5；令y=0，得到x=-
．
因此直线l与坐标轴的交点坐标分别为（0，5），(-
，0)．
∴直线l的方程为：y-3=2（x+1），化为2x-y+5=0．
令x=0，得到y=5；令y=0，得到x=-
| 5 |
| 2 |
因此直线l与坐标轴的交点坐标分别为（0，5），(-
| 5 |
| 2 |
点评：本题考查了直线的点斜式方程及直线与坐标轴的交点坐标，属于基础题．
练习册系列答案
字词句段篇系列答案
相关题目
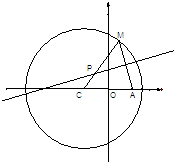如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P是线段AM的垂直平分线与直线CM的交点．