题目内容
利用秦九韶算法求多项式f（x）=3x6+4x5-5x4-7x2+8x+1在x=2时的值，写出详细步骤．
考点：秦九韶算法,中国古代数学瑰宝
专题：算法和程序框图
分析：f（x）=3x6+4x5-5x4-7x2+8x+1=（（（（（3x+4）x-5）x）x-7）x+8）x+1．
计算在x=2时的值，v0=3，v1=3×2+4=10，…，依此类推可得v2=15，v3=30，v4=53，v5=114，v6=229．
计算在x=2时的值，v0=3，v1=3×2+4=10，…，依此类推可得v2=15，v3=30，v4=53，v5=114，v6=229．
解答：
解：f（x）=3x6+4x5-5x4-7x2+8x+1=（（（（（3x+4）x-5）x）x-7）x+8）x+1
计算在x=2时的值，v0=3，
v1=3×2+4=10，
v2=10×2-5=15，
v3=15×2=30，
v4=30×2-7=53，
v5=53×2+8=114，
v6=114×2+1=229．
故当x=2时，f（2）=229．
计算在x=2时的值，v0=3，
v1=3×2+4=10，
v2=10×2-5=15，
v3=15×2=30，
v4=30×2-7=53，
v5=53×2+8=114，
v6=114×2+1=229．
故当x=2时，f（2）=229．
点评：本题考查了根据“秦九韶算法”求多项式的值，属于基础题．
练习册系列答案
相关题目
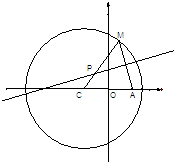如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P是线段AM的垂直平分线与直线CM的交点．