Question

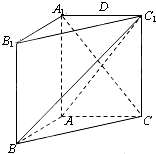如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=AC=2AB=2，且BC₁⊥A₁C．
（Ⅰ）求证：平面ABC₁⊥平面A₁C₁CA；
（Ⅱ）设D是A₁C₁的中点，判断并证明在线段BB₁上是否存在点E，使DE∥平面ABC₁；若存在，求三棱锥E-ABC₁的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,平面与平面垂直的判定

专题：综合题,空间位置关系与距离

分析：（Ⅰ）证明平面ABC₁⊥平面A₁C，只需证明A₁C⊥平面ABC₁；
（Ⅱ）取AA₁中点F，连EF，FD，证明平面EFD∥平面ABC₁，则有ED∥平面ABC₁，利用等体积转换，可求三棱锥E-ABC₁的体积．

解答： （I）证明：在直三棱柱ABC-A₁B₁C₁中，有AA₁⊥平面ABC．
∴AA₁⊥AC，又AA₁=AC，∴A₁C⊥AC₁．             …（2分）
又BC₁⊥A₁C，∴A₁C⊥平面ABC₁，
∵A₁C?平面A₁C₁CA，
∴平面ABC₁⊥平面A₁C₁CA．    …（4分）
（II）解：取AA₁中点F，连EF，FD，当E为B₁B中点时，EF∥AB，DF∥AC₁．
即平面EFD∥平面ABC₁，则有ED∥平面ABC₁．…（8分）
当E为中点时，V _E-ABC1=V_C1-ABE=

1

3

•2•

1

2

•1•1=

1

3

．

点评：本小题主要考查利用线面垂直的判定定理证明线面垂直，考查体积的计算，并且考查空间想象能力和推理论证能力，属于中档题．