题目内容
已知函数f(x)=lnx-ax2+2bx(a>0),且f′(1)=0
(1)求函数f(x)的单调递增区间;
(2)试问函数f(x)图象上是否存在两点A(x1,y1),B(x2,y2),其中x2>x1,使得函数f(x)在x=
的切线与直线AB平行?若存在,求出A,B的坐标,不存在说明理由.
(1)求函数f(x)的单调递增区间;
(2)试问函数f(x)图象上是否存在两点A(x1,y1),B(x2,y2),其中x2>x1,使得函数f(x)在x=
| x1+x2 |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求函数的定义域和导数,根据f′(x)>0,即可求函数f(x)的单调递增区间;
(2)求出函数的导数,利用导数的几何意义,以及直线平行的性质,即可得到结论.
(2)求出函数的导数,利用导数的几何意义,以及直线平行的性质,即可得到结论.
解答:
解:(1)∵函数f(x)的定义域为(0,+∞),
∴f′(x)=
-2ax+2b,
又f′(1)=0,∴有2b=2a-1,
∴f′(x)=
-2ax+2a-1=-(x-1)(2a+
),
又a>0,x>0,∴f′(x)>0有0<x<1,
即f(x)的单调递增区间为(0,1).
(2)根据条件y1=lnx1-a
+(2a-1)x1,y2=lnx2-ax22+(2a-1)x2,
即kAB=
=
-a(x1+x2)+(2a-1),
而f′(
)=
-a(x1+x2)+(2a-1)=kAB,
则整理可得
=
,
即有ln
=
,
令
=t(0<t<1),即lnt+
-2=0,
令g(t)=lnt+
-2(0<t≤1),则g′(t)=
≥0,
则函数g(t)在(0,1]上单增,而g(1)=0,
∴在(0,1)内,g(t)<0,
即lnt+
-2=0在(0,1)内无解,
故不存在.
∴f′(x)=
| 1 |
| x |
又f′(1)=0,∴有2b=2a-1,
∴f′(x)=
| 1 |
| x |
| 1 |
| x |
又a>0,x>0,∴f′(x)>0有0<x<1,
即f(x)的单调递增区间为(0,1).
(2)根据条件y1=lnx1-a
| x | 2 1 |
即kAB=
| y1-y2 |
| x1-x2 |
| lnx1-lnx2 |
| x1-x2 |
而f′(
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
则整理可得
| lnx1-lnx2 |
| x1-x2 |
| 2 |
| x1+x2 |
即有ln
| x1 |
| x2 |
2(
| ||
(
|
令
| x1 |
| x2 |
| 4 |
| t+1 |
令g(t)=lnt+
| 4 |
| t+1 |
| (t-1)2 |
| t(t+1)2 |
则函数g(t)在(0,1]上单增,而g(1)=0,
∴在(0,1)内,g(t)<0,
即lnt+
| 4 |
| t+1 |
故不存在.
点评:本题主要考查函数单调性的判断,利用导数的应用是解决本题的关键.考查学生的运算能力.

练习册系列答案
相关题目
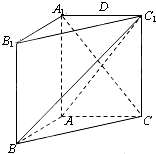 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.