题目内容

斜率为3的直线经过抛物线x2=8y的焦点，且与抛物线相交于A，B两点，求线段AB的长．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设直线l的倾斜角为α，则l与y轴的夹角θ=90°-α，
1
tanθ
=tanα=2，sinθ=
3
10
，由此能求出|AB|．
解答： 解：设直线l的倾斜角为α，则l与y轴的夹角θ=90°-α，
∴
1
tanθ
=tanα=3，
∴sinθ=
3
10
，
∴|AB|=
8
sin2θ
=
80
9
．
点评：本题考查抛物线的焦点弦的求法，解题时要注意公式的灵活运用．
练习册系列答案
相关题目
已知椭圆的焦点F1、F2在x轴上，它与y轴的一个交点为P，且△PF1F2为正三角形，且椭圆上的点与焦点的最短距离为
3
，则椭圆的方程为（　　）
A、
x2
12
+
y2
9
=1
B、
x2
25
+
y2
9
=1
C、
x2
40
+
y2
10
=1
D、
y2
25
+
4x2
25
=1
已知数列{an}满足a1=4，an+1-4an=4n（n∈N*），数列{bn}满足bn=
an
4n

（Ⅰ）求证：数列{bn}是等差数列；
（Ⅱ）设Sn=
a1
4
+
a2
5
+
a3
6
+…+
an
n+3
，求满足不等式
1
257
＜
Sn
S2n
＜
1
5
的所有正整数n的值．
已知函数f（x）=x3-ax2-3x，a∈R．
（1）若f（x）在区间[1，+∞）上是增函数，求a的取值范围；
（2）若f （x）在区间 （-1，2）内存在两个极值点，求a的取值范围．
已知函数f（x）=x2+alnx．
（1）当a=-2e时，求函数f（x）的单调区间；
（2）若函数g（x）=f（x）-2x在[1，4]上是减函数，求实数a的取值范围．
已知焦点在x轴上椭圆长轴是短轴的2倍，椭圆上任意一点与两焦点组成的三角形面积的最大值为
3
，P是圆x2+y2=16上任意一点，过P点作椭圆的切线PA，PB，切点分别为A，B．
（1）求椭圆的轨迹方程；
（2）求
PA
•
PB
的最大值和最小值．
已知Sn是数列{an}的前n项和，an＞0，且Sn=
an2+an
2
（n∈N*）
（Ⅰ）求证数列{an}是等差数列；
（Ⅱ）设数列{bn}满足bn=
1
Sn
，求数列{bn}的前n项和．
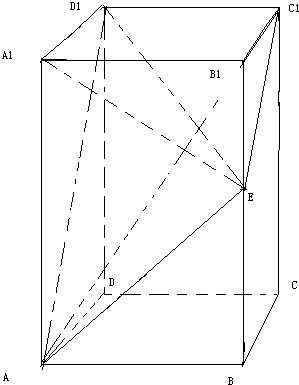长方体ABCD-A1B1C1D1中，AB=AD=1，BB1=2，E为BB1的中点．（1）求证：AE⊥平面A1D1E；
（2）求二面角E-AD1-A1的正切值；
（3）求三棱锥A-C1D1E的体积．
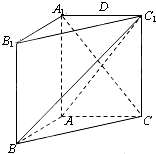如图，在直三棱柱ABC-A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
（Ⅰ）求证：平面ABC1⊥平面A1C1CA；
（Ⅱ）设D是A1C1的中点，判断并证明在线段BB1上是否存在点E，使DE∥平面ABC1；若存在，求三棱锥E-ABC1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网