题目内容
已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1.
1)求{an}、{bn}的通项公式;
2)若cn=anbn,{cn}的前n项和为Tn,求Tn.
1)求{an}、{bn}的通项公式;
2)若cn=anbn,{cn}的前n项和为Tn,求Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式能求出首项和公差,由此能求出an=2n-1(n∈N*);由Sn=2bn-1
,能推导出{bn}是首项为1公比为2的等比数列,由此求出bn=2n-1(n∈N*).
(2)由cn=anbn=(2n-1)•2n-1,利用错位相减法能求出{cn}的前n项和为Tn.
,能推导出{bn}是首项为1公比为2的等比数列,由此求出bn=2n-1(n∈N*).
(2)由cn=anbn=(2n-1)•2n-1,利用错位相减法能求出{cn}的前n项和为Tn.
解答:
解:(1)∵{an}是等差数列,且a3=5,a7=13,设公差为d.
∴
,解得
∴an=1+2(n-1)=2n-1(n∈N*)
在{bn}中,∵Sn=2bn-1
当n=1时,b1=2b1-1,∴b1=1
当n≥2时,由Sn=2bn-1及Sn-1=2bn-1-1,
得bn=2bn-2bn-1,∴bn=2bn-1
∴{bn}是首项为1公比为2的等比数列
∴bn=2n-1(n∈N*)
(2)∵cn=anbn=(2n-1)•2n-1,
∴Tn=1+3•2+5•22+…+(2n-1)•2n-1①2Tn=1•2+3•22+5•23+…+(2n-3)•2n-1+(2n-1)•2n②
①-②得 -Tn=1+2•2+2•22+…+2•2n-1-(2n-1)•2n
=1+2•
-(2n-1)•2n
=1+4(2n-1-1)-(2n-1)•2n=-3-(2n-3)•2n
∴Tn=(2n-3)•2n+3(n∈N*)
∴
|
|
∴an=1+2(n-1)=2n-1(n∈N*)
在{bn}中,∵Sn=2bn-1
当n=1时,b1=2b1-1,∴b1=1
当n≥2时,由Sn=2bn-1及Sn-1=2bn-1-1,
得bn=2bn-2bn-1,∴bn=2bn-1
∴{bn}是首项为1公比为2的等比数列
∴bn=2n-1(n∈N*)
(2)∵cn=anbn=(2n-1)•2n-1,
∴Tn=1+3•2+5•22+…+(2n-1)•2n-1①2Tn=1•2+3•22+5•23+…+(2n-3)•2n-1+(2n-1)•2n②
①-②得 -Tn=1+2•2+2•22+…+2•2n-1-(2n-1)•2n
=1+2•
| 2(1-2n-1) |
| 1-2 |
=1+4(2n-1-1)-(2n-1)•2n=-3-(2n-3)•2n
∴Tn=(2n-3)•2n+3(n∈N*)
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
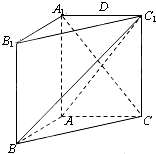 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.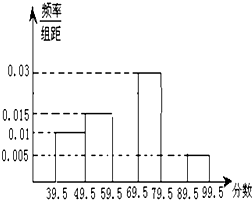 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题: