题目内容
已知（1-2x）2014=a0+a1x+a2x2+…+a2014x2014，则a1+2a2+3a3+…+2014a2014= ．
考点：二项式系数的性质
专题：二项式定理
分析：由条件可得-4028（1-2x）2013 =a1+2a2x+…+a2014x2013 ①，在等式①中，令x=1，可得a1+2a2+3a3+…+2014a2014的值．
解答：
解：∵（1-2x）2014=a0+a1x+a2x2+…+a2014x2014，
两边分别对x求导数，可得-4028（1-2x）2013=a1+2a2x+…+a2014x2013 ①．
在等式①中，令x=1，可得a1+2a2+3a3+…+2014a2014=4028，
故答案为：4028．
两边分别对x求导数，可得-4028（1-2x）2013=a1+2a2x+…+a2014x2013 ①．
在等式①中，令x=1，可得a1+2a2+3a3+…+2014a2014=4028，
故答案为：4028．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
名校课堂系列答案
相关题目
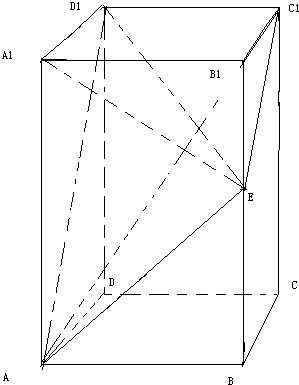长方体ABCD-A1B1C1D1中，AB=AD=1，BB1=2，E为BB1的中点．（1）求证：AE⊥平面A1D1E；
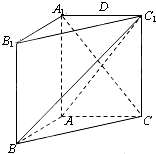如图，在直三棱柱ABC-A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．