题目内容
若a＜b＜0，则下列不等关系中，不能成立的是（ ）
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|
考点：不等关系与不等式
专题：不等式的解法及应用
分析：利用不等式的性质即可得出．
解答：
解：∵a＜b＜0，
则a＜a-b＜0，a（a-b）＞0，
∴
＜
，化为
＜
．
因此B不成立．
故选：B．
则a＜a-b＜0，a（a-b）＞0，
∴
| a |
| a(a-b) |
| a-b |
| a(a-b) |
| 1 |
| a-b |
| 1 |
| a |
因此B不成立．
故选：B．
点评：本题考查了不等式的性质，属于基础题．
练习册系列答案
相关题目
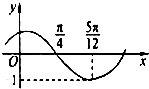函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|
下列命题错误的是（ ）
| A、命题“若m≤0，则方程x2+x+m=0有实数根”的逆否命题为：“若方程x2+x+m=0无实数根，则m＞0” |
| B、“x=2”是“x2-x-2=0”的充分不必要条件 |
| C、若命题“p且q”为假命题，则命题“p”与命题“q”中必有一真一假 |
| D、对于命题p：存在x∈R，x2+x+1＜0，则非p：对任意x∈R，x2+x+1≥0 |
（x2+
）6的展开式中x3的系数是（ ）
| 2 |
| x |
| A、20 | B、160 |
| C、240 | D、60 |
已知0＜α＜
＜β＜π，tan
=
，cos（α-β）=
，则β的值为（ ）
| π |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=x3+
（x∈R），f（x1）+f（x2）＞0，则下列不等式中正确的是（ ）
| 2x-1 |
| 2x+1 |
| A、x1＞x2 |
| B、x1＜x2 |
| C、x1+x2＞0 |
| D、x1+x2＜0 |
设x=30.5，y=log32，z=cos2，则（ ）
| A、z＜y＜x |
| B、z＜x＜y |
| C、y＜z＜x |
| D、x＜z＜y |
求证：
+
＞
．
证明：因为
+
和
都是正数，
所以为了证明
+
＞
，
只需证明（
+
）2＞（
）2，
展开得5+2
＞5，即2
＞0，显然成立，
所以不等式
+
＞
．上述证明过程应用了（ ）
| 2 |
| 3 |
| 5 |
证明：因为
| 2 |
| 3 |
| 5 |
所以为了证明
| 2 |
| 3 |
| 5 |
只需证明（
| 2 |
| 3 |
| 5 |
展开得5+2
| 6 |
| 6 |
所以不等式
| 2 |
| 3 |
| 5 |
| A、综合法 | B、分析法 |
| C、综合法、分析法混合 | D、间接证法 |
函数y=sin2（
+x）-sin2（
-x）的值域是（ ）
| π |
| 4 |
| π |
| 4 |
| A、[-1，0] | ||
| B、[0，1] | ||
| C、[-1，1] | ||
D、[-
|