题目内容
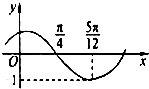函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据图象求出φ的值，再由“左加右减”法则判断出函数图象平移的方向和单位长度．
解答：
解：∵选项只与平移有关，没有改变函数图象的形状，故ω=3，
又函数的图象的第二个点是（
，0）
∴3×
+φ=π
于是φ=
，则f（x）=Asin（3x+
）
故g（x）=Asin3x=Asin[3（x-
）+
]
∴函数的图形要向右平移
个单位，
故答案为：C．
又函数的图象的第二个点是（
| π |
| 4 |
∴3×
| π |
| 4 |
于是φ=
| π |
| 4 |
| π |
| 4 |
故g（x）=Asin3x=Asin[3（x-
| π |
| 12 |
| π |
| 4 |
∴函数的图形要向右平移
| π |
| 12 |
故答案为：C．
点评：本题主要考查了三角函数的函数图象，根据函数图象求解析式时，注意应用正弦函数图象的关键点进行求解，考查了读图能力和图象变换法则，属于中档题．
练习册系列答案
相关题目
阅读如图程序：
如果输入x=-2，则输出结果y为（ ）
如果输入x=-2，则输出结果y为（ ）
| A、π-5 | B、-π-5 |
| C、3+π | D、3-π |
用数学归纳法证明：1+
+
+…+
＜2-
（n∈N*），第二步证明“从k到k+1”，左端增加的项数是（ ）
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (2n)2 |
| 1 |
| 2n |
| A、1 | B、2 | C、2k | D、8k+4 |
当x∈（0，
）时，下面四个函数中最大的是（ ）
| π |
| 4 |
| A、sin（cosx） |
| B、sin（sinx） |
| C、cos（sinx） |
| D、cos（cosx） |
设复数z=1-3i，z的共轭复数是
，则|
|=（ ）
. |
| z |
| z | ||
|
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
若2
，2
，2
成等比数列，则点（ x，y ）在平面直角坐标系内的轨迹是（ ）
| 3x |
| x+y |
| x+1 |
| A、一段圆弧 |
| B、椭圆的一部分 |
| C、双曲线一支的一部分 |
| D、抛物线的一部分 |
若a＜b＜0，则下列不等关系中，不能成立的是（ ）
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|