题目内容
(x2+
)6的展开式中x3的系数是( )
| 2 |
| x |
| A、20 | B、160 |
| C、240 | D、60 |
考点:二项式系数的性质
专题:二项式定理
分析:按照二项式定理写出二项式的通项,整理后使x的指数为3,找到对应的r值,计算系数即可.
解答:
解:(x2+
)6的展开式的通项为Tr+1=
(x2)6-r(
)r=2r
x12-3r,令12-3r=3解得r=3,∴x3的系数为
=160;
故选B.
| 2 |
| x |
| C | r 6 |
| 2 |
| x |
| C | r 6 |
| 23C | 3 6 |
故选B.
点评:本题考查了二项式定理的运用;要求二项展开式的特征项,只要明确二项展开式的通项,从字母的指数入手,得到相应的使要求成立的值.

练习册系列答案
相关题目
阅读如图程序:

如果输入x=-2,则输出结果y为( )

如果输入x=-2,则输出结果y为( )
| A、π-5 | B、-π-5 |
| C、3+π | D、3-π |
若2
,2
,2
成等比数列,则点( x,y )在平面直角坐标系内的轨迹是( )
| 3x |
| x+y |
| x+1 |
| A、一段圆弧 |
| B、椭圆的一部分 |
| C、双曲线一支的一部分 |
| D、抛物线的一部分 |
某2列联表为:
则x与y之间有关系的可能性为( )
| y1 | y2 | |
| x1 | 5 | 15 |
| x2 | 40 | 10 |
| A、0.1% | B、99.9% |
| C、97.5% | D、0.25% |
数列{an}满足a1=1,an+4an-1=0(n≥2),则a2与a4的等比中项是( )
| A、4 | B、±4 | C、16 | D、±16 |
若函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω和φ的取值是( )
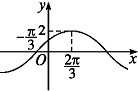

A、ω=
| ||||
B、ω=
| ||||
C、ω=1,φ=-
| ||||
D、ω=1,φ=
|
若a<b<0,则下列不等关系中,不能成立的是( )
A、
| ||||
B、
| ||||
C、a
| ||||
D、a
|
已知椭圆准线x=4对应焦点(2,0),离心率e=
,则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
| B、3x2+y2+28y+60=0 | ||||
| C、3x2+4y2-8x=0 | ||||
| D、2x2+3y2-7x+4=0 |
下列命题中,真命题是( )
| A、空间不同三点确定一个平面 |
| B、空间两两相交的三条直线确定一个平面 |
| C、两组对边相等的四边形是平行四边形 |
| D、和同一直线都相交的三条平行线在同一平面内 |